[통계 데이터분석] 공분산분석, 반복측정 분산분석, 다변량 분산분석
1. 공분산분석
- 공분산분석) 분산분석에 공변량을 추가하여 분산분석모델을 확장함.
( 분산분석 = 집단 간의 차이 검정
-> 예- 분산분석을 이용해서 '세 종류의 비만치료제 간의 효과가 차이가 있는지' 검정 가능.
그런데, 비만은 '스트레스'와 밀접한 관련이 있음. 그리고 '3가지 치료제 집단'의 포함된 참여자들의 스트레스 수준은 서로 다를 수 있음'
=> 일원분산분석을 통해 '비만치료제 간의 치료효과의 차이가 있다'고 결론을 내렸으면,
그 이유는 '치료제' 때문 만이 아니라, 어쩌면 '참여자들의 스트레스 수준의 차이'가 영향을 미쳤을 수도 있음
-> 참여자의 스트레스 수준을 사전에 측정해서, 참여자들의 스트레스 수준을 통제해서 '치료제의 인한 순수한 차이'를 검정 가능!
-> 스트레스 영향을 배제한 상태 = 스트레스 수준 일정한 상태) 치료제 간의 차이가 존재하는지 검증
-> 스트레스 수준 = 공변량/ 공변량을 모델에 포함시켜서 분산분석 모델을 확장한 것을 '공분산 분석'
(공변량 = 연속형 변수를 가정함)
- sexab 데이터셋 : 아동기의 성폭력 경험이 성인의 정신건강에 미치는 영향을 분석한 연구에 사용됨
library(faraway)
str(sexab)
-> 아동기에 성폭력을 경험했는지 여부에 따라 성인 여성을 두 개의 집단으로 구분하였음
- csa 변수 : 독립변수인 집단변수로서 '아동기의 성폭력 경험'을 나타내며, 성폭력을 경험했으면 'Abused' 로 코딩되었고, 경험하지 않았으면 'NotAbused' 로 코딩되었음
- ptsd 변수 : 종속변수로서 '외상 후 스트레스 장애'를 나타냄
- cpa 변수 : 공변량으로서 아동기의 신체적 학대를 의미함
-> [아동기의 성폭력 경험 유무가 성인의 외상 후 스트레스 장애에 미치는 순수한 영향 관계 분석]
- 평균, 표준편차, 표본크기 등 집단별 (즉, 성폭력 경험 유무별) 요약통계량
# tapply() 함수의 첫번째 인수 = 대상 벡터 지정
# tapply() 함수의 두번째 인수 = 집단 변수 지정
# tapply() 함수의 세번째 인수 = 집단별로 적용할 함수 지정
tapply(sexab$ptsd, sexab$csa, mean)
tapply(sexab$ptsd, sexab$csa, sd)
tapply(sexab$ptsd, sexab$csa, length) #집단별 관측값 갯수

-> lenght() 함수 = 76 명의 여성 가운데 45명은 아동기에 성폭력 경험이 있으며, 나머지 31명은 그러한 경험을 겪지 않았음.
[평균값] '외상 후 스트레스 장애 정도'는 '아동기의 성폭력 경험 유무'에 따라 큰 차이가 있었음.
-> 아동기에 성폭력을 경험한 여성이 그렇지 않은 여성에 비해 '두 배 이상 높은 외상 후 스트레스 장애'를 겪는 것으로 나타남
[ 아동기의 성폭력 경험과 외상 후 스트레스 장애 간의 관계를 통계적으로 검정 ]
- 외상 후 스트레스 장애는 아동기의 성폭력 경험뿐만 아니라 신체적 학대에 의해서도 영향을 받을 것으로 예상되므로 아동기의 신체적 학대를 공변량으로 모델에 투입하여 통제함으로써 '아동기의 성폭력 경험과 외상 후 스트레스 장애 간의 순수한 영향관계를 분석함'
- aov( ) 함수 = 일원공분산분석 수행
# 성인의 ptsd 가 성폭력만이 영향을 끼치는가? (다른 요인은?)=> 순수한 효과만 확인하고자할 때!
# 공분산: cpa_ 어렸을 때 신체적 학대!
# 신체적 학대 + 성폭력 => 더 큰 영향을 끼치지 않을까?
# 순서가 중요! (공변량 먼저! + csa_ 진짜 궁금한 변수)
# aov()함수의 첫번째 인수(포뮬러) = 종속변수(ptsd) ~ 독립변수(집단 독립변수 csa)
# aov()함수의 두번째 인수 = 데이터셋 지정
sexab.aov <- aov(ptsd ~ csa, data=sexab)
summary(sexab.aov)
-> 귀무가설 기각) [대립] 아동기의 성폭력 경험에 따라서 외상 후 스트레스 장애는 차이가 있다 (영향을 미침)
=> '외상 후 스트레스 장애'는 아동기의 성폭력 경험 뿐만 아니라, '아동기의 신체적 학대'에 있어서도 영향을 받을 것이다.
=> 아동기의 성폭력 경험이 '외상 후 스트레스 장애'에 미치는 순수한 영향을 파악하기 위해서, '아동기의 신체적 학대'의 영향을 살펴봐야 함!
[공분산분석]
-> '아동기의 신체적 학대가 일정하다' 는 가정 하에서 '아동기의 성폭력 경험'과 외상 후 스트레스 장애 간의 순수한 관계 파악
# aov()함수의 첫번째 인수(포뮬러) = 종속변수(ptsd) ~ 독립변수(공변량 cpa+ 집단 독립변수 csa)
# aov()함수의 두번째 인수 = 데이터셋 지정
sexab.aov <- aov(ptsd ~ cpa + csa, data=sexab)
summary(sexab.aov)
-> 분산분석표 ) 공변량 cpa 와 독립변수 cas 의 p 값이 유의수준 0.05 에 비해 매우 작음
-> 아동기의 신체적 학대는 외상 후 스트레스 장애와 관련이 있으며, 또 아동기의 신체적 학대를 통제한 상태에서 아동기의 성폭력 경험은 외상 후 스트레스 장애에 영향을 미침.
-> 즉, 외상 후 스트레스 장애에 영향을 미치는 '신체적 학대'를 통제한 후에도 '아동기에 성폭력을 경험한 집단'과 그렇지 않은 집단은 '외상 후 스트레스 장애'에 있어서 통계적으로 유의한 차이를 나타냄
# 해석: csa(집단변수) -> 통계적으로 유의하다_유의수준 0.05 에 비해 작다 (ptsd 차이가 있음!)
# 해석: cpa -> 통계적으로 유의함 (ptsd에 영향을 미침!)
# => cpa(신체적 학대)의 영향이 있음에도 불구하고 여전히 csa 의 영향도 존재함!
# if) cpa+ csa 일때, csa가 아닌 cpa 영향만 있을 땐 csa 의 p 값이 통계적으로 유의하지 않을 것!
- effect( )함수 = 공변량 (아동기의 신체적 학대_cpa)의 영향을 제거한 후의 조정된 '외상 후 스트레스 장애'의 집단 평균 계산
*tapply( ) 함수를 이용하여 구한 조정 전의 집단평균에 비하여 '성폭력 경험 집단'은 약간 낮아졌고, 반대로 성폭력 비경험 집단은 조금 높아졌음*
library(effects)
# effect() 함수의 첫번째 인수 = 집단 변수 지정
# effect() 함수의 두번째 인수 = 공분산 분석 결과 생성된 모델 객체 지정
effect("csa", sexab.aov)
-> 앞서 tapply( )함수를 이용해서 구한 '조정 전의 집단 평균'에 비해서 '성폭력 경험 집단'은 약간 낮아졌고, 반대로 '성폭력 경험 집단'은 약간 높아졌음
-> 공변량인 '아동기의 신체적 학대'에 영향을 제거하면, 아동기에 성폭력을 경험한 집단과 그렇지 않은 집단 간의 '외상 후 스트레스 장애'의 평균값의 차이가 미미하긴 하지만, 좀전에 비해서 작아지는 것을 볼 수 있음
- ancova( ) 함수 = 공분산분석 결과 그래프 출력
library(HH)
windows(width=7.0, height=5.5)
ancova(ptsd ~ cpa + csa, data=sexab)

- x 축 = (공변량) 아동기의 신체적 학대
- y 축 = (종속 변수) 외상 후 스트레스 장애
- 구분 = (독립변수) 아동기의 성폭력 경험 유무에 따른 각각의 별도의 패널에 집단 별로 그래프가 생성되어 있음
(왼쪽) 아동기의 성폭력 경험이 있는 집단/ (오른쪽) 아동기의 성폭력 경험이 없는 집단
-> 아동기의 신체적 학대로부터 '외상 후 스트레스 장애'를 예측하는 이 두 개의 회귀선은, '두 집단 모두에서 동일한 기울기를 가지면서 절편은 서로 다르게 편이 되어있음
-> 2개의 회귀선의 기울기가 같은 이유= 아동기의 신체적 학대 수준이 '외상 후 스트레스 장애'에 미치는 영향이, 두 집단에서 일정하도록 공변량을 통제 했기 때문에!
(공분산분석도표) 아동기 신체적 학대(cpa) 경험이 증가할수록, 외상 후 스트레스 장애 (ptsd)가 증가하며, 아동기 성폭력(cpa) 경험 집단이 그렇지 않은 집단보다 더 큰 외상 후 스트레스 장애를 겪음
* 기울기가 같은 이유, 일정한 비율로 영향을 미치게 하도록 통제!

- ancova( ) 함수 = 종속변수, 공변량, 독립변수 간의 관계를 그래프로 보여줌
-> 아동기 신체적 학대(cpa)로부터 '외상 후 스트레스 장애(ptsd)'를 예측하는 회귀선은 두 집단 모두에서 동일한 기울기를 가지나 절편을 서로 다름. 아동기 신체적 학대 경험이 증가할수록 외상 후 스트레스 장애 역시 증가함.
또한 아동기 성폭력 경험 집단이 그렇지 않은 집단보다 더 큰 외상 후 스트레스 장애를 겪음
2. 반복측정 분산분석
- 반복측정 분산분석) 하나의 실험 대상에 대해 두 번 이상 반복측정한 관측값 간의 차이 검정
= 동일한 대상에 대해 여러 번 반복측정하여 반복측정 집단 간에 차이가 존재하는지 검정
- 평균검정 -> 대응 표본 검정) 동일한 대상에 대해서 두 차례 측정해서 , 2개의 대응 표본 간의 차이를 검증
- 반복측정 분산분석) 반복 측정 횟수를 3번 이상으로 확장해서 3개 이상의 집단 간의 차이 검정
- 일반적 형태의 분산분석 = 다른 집단에 속한 대상들 간의 '집단 간 차이'를 분석하는 것
- 반복측정 분산분석 = 동일 집단에 속한 대상들 간의 '집단 내 차이'를 규명하는 것

[10명의 우울증 환자에 대해서 심리치료를 실시하고, 심리치료 효과가 기간에 따라서 변화가 있었는지에 대한 검정]
-> 집단 간 요인 과 집단 내 요인이 각각 한 개씩인 반복측정 이원분산분석 을 살펴봄
- 집단 내 요인= 동일한 대상에 대해서 반복 측정한 결과를 구분하는 변수 (기간 변수)
- 집단 간 요인= 대상을 서로 구분되는 집단으로 분할하는 변수 (심리치료 변수)
-> ' 집단 간 요인' 과 '집단 내 요인' 모두 집단변수로서의 역할을 수행하며, 집단 내 요인의 각 범주별로 반복측정한 값이 저장됨
- co2 데이터셋 = 식물이 저온의 생장환경에서 견디는 정도를 나타내는 저온내성 실험을 위해 수집된 데이터셋
* 퀘백 지역의 여섯 개 나무와 미시시피 지역의 여섯 개 나무의 이산화탄소 흡수율을 7개의 서로 다른 이산화탄소 농도 하에서 반복측정함*
* 퀘백 지역 나무의 절반과 미시시피 지역 나무의 절반은 실험 전에 하룻밤 동안 저온처리를 함! (저온처리가 적용된 나무만을 대상으로 함)
-> 퀘백 지역 나무와 미시시피 나무 간의 '이산화탄소 흡수율'의 차이 검정
-> 7 개의 서로 다른 이산화탄소 농도에 따라서 '이산화탄소 흡수율'이 차이가 있는지도 검정
-> 나무의 출신 지역과 이산화탄소 흡수율 간의 관계가 '이산화탄소 농도'에 따라서 달라지는지 검정
- 종속변수 = 이산화탄소 흡수율(uptake)
- 독립변수(범주형 변수) = 나무의 출신 지역 (type)과 이산화탄소 농도(conc) -> 이원분산분석
- -> type 변수 = 집단 간 요인/ conc 변수 = 반복적으로 측정된 값 (집단 내 요인)
#퀘백 지역의 나무(추운지역) vs 미시시피 (따뜻한 지역)의 나무 -> 이산화탄소 흡수율 차이 검정
# 심리치료 (퀘백나무, 미시시피 나무), 기간(이산화탄소 흡수율?)
head(CO2, 3); tail(CO2, 3)
CO2sub <- subset(CO2, Treatment=="chilled") #chilled= 저온 처리
CO2sub$conc <- factor(CO2sub$conc) #범주형 변수로 만들기:factor (흡수율)
str(CO2sub)

- 나무의 출신 지역 = 퀘백, 미시시피 (두 개의 범주로 구성됨)
- 이산화탄소 농도 = 일곱 개의 범주로 구성됨
- Type (집단 간 요인- 범주형 변수), conc (집단 내 요인) -> 펙터 형식으로 변환!
[반복측정 이원분산분석]
-> W (집단 내 요인)/ B (집단 간 요인) 의미함-> Subject 변수 = 각 측정 대상에 대한 식별자 변수를 나타냄
* W, B , Subject = 범주형 변수
- 반복측정 일원분산분석: y ~ W + Error (Subject/ W)
- 반복측정 이원분산분석: y ~ B * W + Error (Subject/W)
- y 와 W 의 관계/ y 와 B* W 의 관계 => 일반적인 일원분산분석과 이원분산분석을 사용하는 '포뮬라 지정 방식'
- Error( ) = 특정 대상에 대한 식별자 변수와 '집단 내 요인 변수' 를 '/' 로 연결해서 지정
- aov( ) 함수 = co2 데이터셋에 대한 반복측정 이원분산분석 수행하는 함수
CO2sub.aov <- aov(uptake ~ Type * conc + Error(Plant/conc), data=CO2sub)
summary(CO2sub.aov)
- 두 개의 주효과(Type, conc)와 상호작용 효과(Type:conc)는 유의수준 0.05 에서 모두 통계적으로 유의함
- > (1) 나무 출신 지역에 따라서 '이산화탄소 흡수율' 에 차이가 존재한다.
-> (2) 이산화탄소 농도에 따라서도 '이산화탄소 흡수율'에 있어 차이가 있다.
-> [상호작용 효과] (3) 나무의 출신 지역과 이산화탄소 농도 간의 '상호작용 효과' 역시 존재한다.
=> 출신 지역과 이산화탄소 흡수율 간의 관계는 '이산화탄소 농도에 따라 달라진다'
#관심이 있는 것[Type:conc]=> 상호작용 효과가 존재함
#-> 종류에 따라서/ 이산화탄소 농도에 따라서(조합) -> 차이 존재!
- boxplot( ) 함수= '주효과와 상호작용효과' 확인
windows(width=7.0, height=5.5)
boxplot(uptake ~ Type * conc, data=CO2sub,
col=c("deepskyblue", "violet"), las=2, cex.axis=0.75,
ylab="Carbon dioxide uptake rate", xlab="",
main="Effects of Plant Type and CO2 on Carbon Dioxide Uptake")
# legend 함수에 '범례'지정 (나무 출신 지역)
legend("topleft", inset=0.02,
legend=c("Quebec", "Mississippi"), fill=c("deepskyblue", "violet"))
- y 축 = 이산화탄소 흡수율
- x 축 = 나무의 출신 지역 유형과 이산화탄소 농도의 조합에 따른 '모든 가능한 범주 조합'
-> (상자도표) 퀘백의 나무가 미시시피의 나무보다 이산화탄소 흡수율이 현저히 더 높으며(주효과), 또한 이산화탄소 농도가 증가함에 따라 이산화탄소 흡수율이 증가하고(주효과), 나무 출신 종류간의 차이는 더 커짐( 이산화탄소의 농도와 나무의 출신 지역 간의 상호작용효과)
# 주효과= 1) 종류에 따라서 2)이산화탄소 농도에 따라서
# 상호작용효과= 상호작용효과가 없으면 '기울기가 같아야 함'
- interaction2wt( ) 함수 = 주효과와 상호작용효과를 두 종류의 도표를 이용하여 보여줌
interaction2wt(uptake ~ conc * Type, data=CO2sub)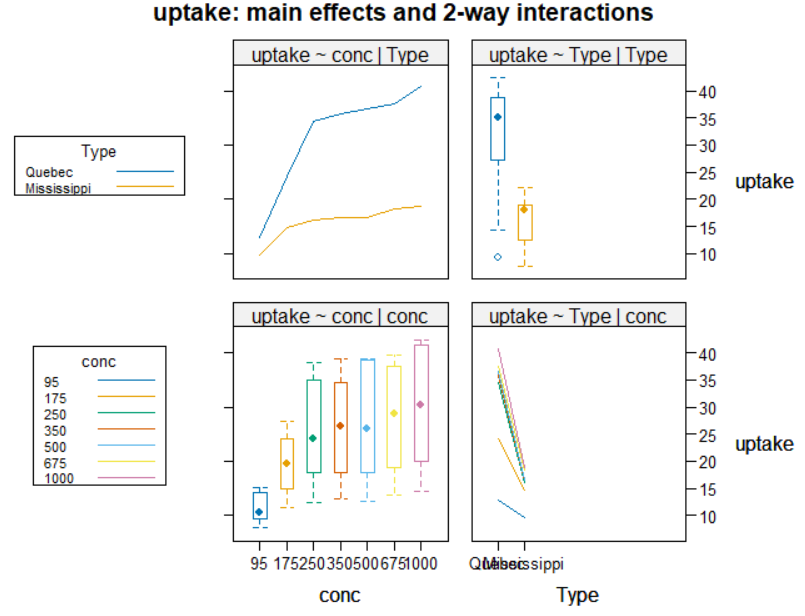
- (상자도표와 선도표) 퀘백의 나무가 미시시피의 나무보다 이산화탄소 흡수율이 현저히 더 높으며, 또한 이산화탄소 농도가 증가함에 따라 그 차이는 더 커짐
-> 퀘백의 나무가 미시시피의 나무보다 이산화탄소 흡수율이 현저히 더 높다 (나무 출신 지역의 주효과),
이산화탄소 농도가 증가할수록 흡수율은 커지는 경향이 있음 (이산화탄소 농도의 주효과),
또한 이산화탄소 농도가 증가함에 따라 퀘백의 나무와 미시시피의 나무 간 이산화탄소 흡수율의 차이는 더 커지는 것을 볼 수 있음
(나무 출신 지역과 이산화탄소 농도의 상호작용효과)
3. 다변량 분산분석
- 두 개 이상의 종속변수가 있을 경우) 다변량 분산분석을 이용하여 집단 간 차이를 동시에 검정 가능 [연구의 타당성 증대]
- Skulls 데이터셋 = 고대 이집트 왕조시대부터 로마시대에 이르기까지 이집트 지역에서 발굴된 인간의 두개골 크기를 측정한 데이터
- epoch 변수 = 이집트 역사에 대한 변수, 다섯 개의 시대로 구분됨 (각 시대 별로 30개 씩의 두개골을 네 개의 지표로 측정)
네 개의 지표 = 두개골의 폭(mb), 높이(bh), 길이 (bl), 코의 높이(nh)
library(heplots)
str(Skulls)
- 데이터셋으로부터, 열개의 관측 값을 무작위로 추출해서 화면에 출력
library(dplyr)
slice_sample(Skulls, n=10)
#sample_n(Skulls, 10)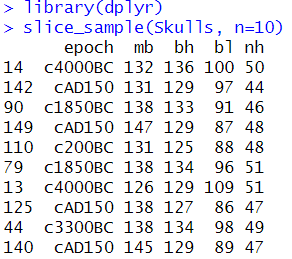
-> 시대별로 4개의 두개골 측정값이 저장되어 있음
[ 다변량 분산분석 ]= 두개골의 측정값이 시대에 따라 다른지 검정
- 독립변수 = 시대 (다섯 개의 범주)
- 종속변수 = 두개골의 폭, 높이, 길이, 그리고 코의 높이
-> (다변량 분산분석 수행) 종속변수들을 결합하여 하나의 행렬 형식으로 변화해야 함
- attach( ) 함수 = 데이터셋의 변수에 접근할 때마다, 데이터셋의 이름을 지정해줘야 하는데, 이러한 불편함을 덜게 하는 함수
=> 사용하는 데이터셋을 '작업 경로'상에 포함 시키기
- cbind( ) 함수 = 두개골의 4개의 측정값을 결합하여 1 행렬 형식으로 변화하는 함수
- aggregate( ) 함수 = 시대별로 두개골 측정값의 평균을 구할 함수
attach(Skulls)
epoch <- Skulls$epoch
y <- with(Skulls, cbind(mb, bh, bl, nh))
# y <- cbind(mb, bh, bl, nh)
aggregate(y, by=list(epoch=epoch), FUN=mean)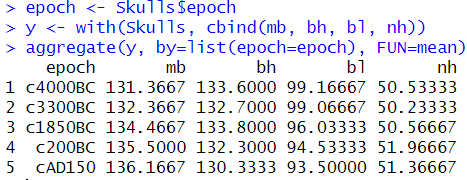
-> 측정 지표에 따라 정도의 차이가 있긴 하지만 대체로 두개골 측정값의 평균이 시대별로 다른듯이 보임
-> 모집단으로 일반화하기 위해선, 통계적 검정 절차가 필요함
- manova( ) 함수 = 종속변수 값(네 가지 유형의 두개골 측정값) 의 집단 (다섯 개 시대) 간 차이에 대한 다변량 분산분석 수행
-> Skulls 데이터셋을 attach 함수를 이용해서 작업 경로 상에 포함시켰기 때문에, 데이터 인수 지정 필요 없음!
# manova()함수의 첫번째 인수 = 종속변수 ~ 독립변수
# -> 종속변수(y)= 두개골 측정값의 행렬 지정/ 독립변수 = 시대를 나타내는 epoch 변수 지정
Skulls.manova <- manova(y ~ epoch)
summary(Skulls.manova)
-> p 값이 유의수준 0.05 에 비해 매우 작으므로, 시대에 따라 두개골 측정값을 다르다고 할 수 있음
- summary.aov( ) 함수 = 일변량 일원분산분석 수행 (어느 두개골 측정값에 차이가 존재하는 확인하기 위한 함수)
summary.aov(Skulls.manova)
-> 유의수준 0.05 에서 nh (코의 높이) 를 제외한 나머지 두개골 측정값은 시대별로 차이가 있음. 시간의 흐름에 따라 두개골 측정값에 차이가 존재한다는 것은 '이민족의 유입에 의한 혼혈의 가능성을 의미함'