[통계 데이터분석] 데이터 요약- 연속형 변수 ⭕

통계

[통계 데이터분석] 데이터 요약- 연속형 변수 ⭕

mming_10 2024. 9. 29. 12:31

범주형 변수->대표값 (최빈값)

연속형 변수= 값을 무한으로 가질 수 있음 -> 대표값을 선정해야 할 필요가 있음 (평균등)

▪️ 중심경향 지표

- 중위수 (median) = 크기 순으로 데이터 값을 정렬했을 떄 중앙에 위치하는 값

( * 데이터 표본의 순서 정보만 이용, 이상치에 의해 왜곡될 가능성은 적으나, 정보의 손실 정도가 클수도 있음*)

- 백분위수 (quantile, percentile) = 백분위의 비율로 분할하는 값

- 사분위수 (quartile) = 25번째, 50번째, 75번째 백분위수 ->

- 평균 (mean) = 데이터 표본에 포함된 관측값을 모두 더한 후 케이스의 개수 (즉 표본의 크기)로 나눈 값

(* 정보의 손실은 적지만, 이상치에 의해 왜곡될 가능성이 큼 * + 합리적으로 판단할 수 있는 수치 )

# 내 성적은 크기 순으로 했을 때 '5번째 백분위수'에 해당됨 '못한 것'(= 내 위에 95명) / 95번째 백분위수 '잘한 것'

▪️ 변동성 지표

- 범위 (range) = 가장 큰 값과 가장 작은 값의 차이

- 사분위 범위 (interquartile range) = 75번째 백분위수와 25번째 백분위수 간의 차이

- 분산 (variance) = 각 관측값이 평균으로부터 떨어져 있는 정도 [ (관측값-평균)^2 들의 합/ 관측 개수 ]

( *원래 관측값의 단위와 무관한 단위로 결과가 나옴 -> 해석 상의 어려움이 있을 수도 *)

( 분산= 0, 전부 같은 값을 가진다는 것을 알 수 있음 )

( 관측값의 단위와 '분산의 단위'가 다름 )

- 표준편차 (standard deviation) = 분산의 제곱근값으로, 실제 값과 동일한 측정단위로 표현할 수 있음

1. 데이터 요약- 연속형 변수

install.packages('MASS')
library(MASS)
str(survey)

1-1. median (중위수) = 크기 순으로 정렬된 데이터셋을 절반으로 분할하는 값

median(survey$Pulse) #중위수 구하기

-> 중간 값이 'NA' 가 아니어도, 데이터셋 중 NA 가 존재하면 'NA' 결과를 냄

median(survey$Pulse, na.rm= TRUE)

- 'na.rm= TRUE' = 중위수 계산 시, NA 계산에서 제외

1-2. [quantile: (중위수와 비슷) 데이터셋을 백분위 비율로 분할하는 값 구하기= 백분위수)]

quantile(survey$Pulse, probs= 0.05, na.rm= TRUE) #5분위수

-> 전체 데이터셋에서 5%에 대응되는 백분위

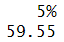
-> 전체 데이터셋에서 50%에 대응되는 백분위수 (중위수와 일치)

quantile(survey$Pulse, probs= 0.5, na.rm= TRUE) #중위수= 50번째 백분위수

- quantile( )함수의 probs 인수에는 벡터를 지정할 수 있음
= 두 개 이상의 비율을 벡터로 지정하게 되면, 해당 비율에 해당하는 백분위수가 출력됨

quantile(survey$Pulse, probs= c(0.05,0.95), na.rm= TRUE)
# = 5번째 백분위수와 95번째 백분위수가 한꺼번에 출력됨

1-3. 사분위수 -> 25번쨰 (첫번째 사분위수), 75번째 (세번째 사분위수)

1st quartile: Q1/ 3rd quartile: Q3

- quantile -> probs 인수에 기본적으로 seq() 함수가 적용되어 있는 걸 볼 수 있음

seq(0, 1, 0.25)

- 0부터 1사이에 0.25 간격으로 5개의 숫자가 출력되는 걸 볼 수 있음

- quantile()함수에는 기본적으로 probs 인수에 다섯 개의 숫자가 지정됨
-> probs 인수를 지정하지 않으면, 저 5개의 인수가 probs 인수에 지정된 것으로 간주됨
-> 5개의 숫자에 대응되는 백분위수를 산출하게 됨

quantile(survey$Pulse, na.rm=TRUE)

- probs 인수에는 5개의 숫자가 기본적으로 적용되기 때문에 '최소값 및 최대값과 함꼐 사분위수'가 출력됨

1-3 (1) 특정 값이 주어졌을 때, 이 값에 대응되는 백분위 비율 구하기

Q. 전체 응답자 중에서 80 이하의 맥박수를 갖고 있는 사람이 전체의 몇퍼센트인가?

-> 논리연산과 평균을 계산한 mean() 함수를 이용할 수 있음 (가장 많이 사용되는 중심경향지표: mean( )함수)

1) 논리연산을 통해서 맥박수 (Pulse)가 80보다 작거나 같은 값이 무언인지를 식별하는 과정을 거치기

survey$Pulse <= 80

(1) 논리연산 실행 시, 맥박수가 80보다 작거나 같은 응답자에 대해서 TRUE 출력

(2) 이후 mean()함수를 이용해서 평균을 계산함

-> mean( )는 TRUE는 1로, FALSE는 0으로 변환해서, 1의 비율을 계산하기 때문에 계산된 평균은 '논리연산 결과 TRUE인 값, 즉 맥박수가 80이하인 값의 비율'을 나타내게 됨

mean(survey$Pulse <= 80, na.rm= TRUE)

-> 75.5% 가 맥박수가 80 이하인 응답자의 비율이 됨

Q. 맥박수의 평균 구하기

mean(survey$Pulse, na.rm= TRUE)

- 맥박수의 평균을 구하기 위해서, 맥박수를 mean()함수의 첫번째 인수로 지정하게 되면 구할 수 있음

2. summary( )함수 이용하기 = 기초 기술통계량 구하기

- 데이터셋에 summary() 함수를 지정하면, '최소값, 최대값, 사분위수, 중위수, 평균과 같은 기초적인 기술 통계량을 구할 수 있음
-> *summary()함수는 적용되는 데이터 형식에 따라서 조금씩 다르게 작동

-> [summary() 함수가 데이터 형식별로 어떻게 작동되는지를 살펴보기]

str(iris)

- iris 데이터셋은 '세종류의 아이리스 꽃에 대해서

(숫자 데이터- 4개 변수) 꽃받침 길이와 꽃잎의 길이 그리고 꽃받침 폭과 꽃잎의 폭을 측정
(factor 데이터: 범주형 데이터터) 아이리스 꽃의 쫓 종류 이름 저장

2 -1. summary() 함수는 인자의 특징에 대해서 '다른 결과'출력

1) summary() 함수에 숫자 벡터 지정

summary(iris$Sepal.Width)

- summary 함수에 'Sepal.Width' 변수를 지정하게 되면
-> 최소값, 첫번째 사분위수, 중위수, 평균, 세번째 사분위수, 그리고 최댓값 출력

2) summary( ) 함수에 펙터를 인수로 지정

summary(iris$Species)

-> 펙터의 레벨(범주별) 빈도를 출력 -> 빈도표 만들기

3) summary () 함수에 문자 벡터 지정

= 펙터인 Species 변수를 문자로 변환해서 지정

summary(as.character(iris$Species))

-> 관측값의 개수 그리고 Class, Mode와 같은 변수 정보 출력

4) 행렬이나 데이터프레임에 summary() 함수를 적용-> 열 단위로 요약통계량 출력

-> 숫자로 구성된 열이면, 6개의 기초적인 통계량 출력
-> 펙터로 구성된 열) 빈도 출력

5) 리스트 데이터 구조에 summary()함수를 적용하게 되면

-> 각 리스트의 원소 크기 & 데이터 형식만 출력

5-1) iris 데이터프레임 데이터셋을 리스트로 변환해서 확인

iris.lst <- as.list(iris)

5-2_ 변환된 리스트 데이터셋을 summary()함수로 넘겨줘서 확인

summary(iris.lst)

-> 각 리스트의 원소 크기 & 데이터 형식만이 출력됨

-> summary( )함수를 통해 얻고자 하는 요약통계량의 정보는 구할 수 없음

-> 리스트 구조로 되어 있는 데이터셋으로부터 요약통계량을 계산하기 위해선, lapply()함수를 이용해서 리스트의 각 원소를 summary()함수로 넘겨줘야 함

6-1) lapply()함수에 리스트 구조의 데이터셋 지정

lapply(iris.lst, summary) #적용함수 'summary' 지정

-> 리스트 구조의 데이터셋에 포함되어 있는 각 원소들이 summary()함수로 넘겨져서 각 원소별로(각 열), 요약통계량 산출

3. range( )함수를 이용해서 범위 계산

- '범위'는 가장 단순한 형태의 변동성 지표로써, 가장 큰 값과 가장 작은 값의 차이를 나타냄

range(survey$Pulse, na.rm= TRUE)

- 맥박수의 최소값이 35, 최대값이 104
-> range()함수는 범위 자체를 출력하지는 않고, 최소값& 최대값만을 출력

3-1. '분산과 표준편차'는 가장 널리 사용되는 변동성지표

(1) 분산은 var()함수를 이용해서 계산

var(survey$Pulse, na.rm= TRUE)

(2) 표준편차는 sd()함수를 이용해서 계산

sd(survey$Pulse, na.rm= TRUE)

4. mtcars 데이터셋 이용(32개의 자동차 모델에 대해 11가지 정보 저장)

str(mtcars)
# mpg) 연비, hp) 마력, wt)무게

4-1. statistics 에 mtcars 데이터셋의 연비하고 마력, 무게- 요약통계량 산출

-> mtcars 데이터셋에 포함되어 있는 mpg, hp, wt 변수에 대해서 요약통계량 확인

install.packages('pastecs')
library(pastecs)
stat.desc(mtcars[c('mpg','hp','wt')])

(1) nbr.val : 관측값의 개수 출력 -> 32개의 자동차

(2) nbr.null : NULL 값의 개수가 출력
(3) nbr.na : NA값의 개수가 출력
# 이 데이터셋에는 NULL & NA 가 포함이 안 되어 있음
(4) SE.mean : 표준오차 계산
(5) 평균의 95% 신뢰구간은 'CI.mean.0.95' 라는 행에 계산되어 있음
(6) 분산 (var), 표준편차 (std.dev), 변동계수 (coef.var)= 표준편차를 평균으로 나눈 지표값

4-2. descirbe()함수를 이용해서 psych패키지가 제공하는 요약통계량 살펴보기

install.packages('psych')
library(psych)

describe(mtcars[c('mpg','hp','wt')])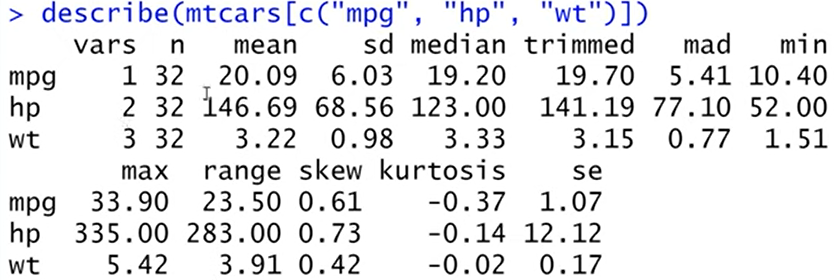

(1) 절삭평균 (trimmed)= 기본값은 상하위 10%를 제외한 10%의 절삭평균을 산출
(2) mad= 중위수 절대편차
(3) 왜도(skew)와 첨도(kurtosis)
-> 왜도= 분포의 치우침 정도, '왜도>0': 정규분포에 비해서 오른쪽으로 긴 꼬리를 갖는 분포를 갖음 (반대도)
-> 첨도= 분포의 뾰족함 정도, 큰 값을 가질수록 정점이 높은 분포를 나타냄 ('첨도>0'이면 정규분포에 비해서 정점이 높은 분포_반대도)
(4) 표준오차: se

개별 변수의 대략적인 특성이나 분포는 평균이나 표준편차와 같은 다양한 기술통계량을 통해서 이해 가능
-> 만약, 데이터셋에 집단을 나타내는 변수가 포함되어 있을 시) 집단별로 기술통계량을 계산하고 비교하는 데에관심을 가짐
-> 집단별로 기술통계량을 계산하게 되면, 집단을 이해하는 데 있어서 종종 유용한 정보를 얻을 수 있음

str(survey)

- survey데이터셋의 변수 중에서, Exer 변수는 운동습관을 나타내는 집단변수 (펙터형식으로 저장)
- 어떤 범주로 구성되어 있는지 확인: levels()

levels(survey$Exer)

-> 운동을 자주하는 사람, 전혀 하지 않는 사람, 약간 하는 사람(응답자의운동습관 구분)
-> 이 범주별로 '연속형 변수의 평균'이나, 표준편차 등 계산 가능

4-3. Pulse 변수를 이용해서 응답자의 평균 계산

(1) [운동습관별 맥박수의 평균 계산]

-> 집단별 기술통계량 계산: tapply() 함수

tapply(survey$Pulse, INDEX= survey$Exer, FUN= mean, na.rm= TRUE)

-> tapply( , )함수: 첫번째 인수에 벡터 형식의 데이터셋 지정/
-> tapply( , )함수: 두번째 인수(INDEX 인수)-> 집단변수(Exer 변수)를 지정
-> tapply( , )함수: 세번째 인수(FUN 인수)-> 집단별로 적용할 통계량 계산 함수 지정

(2) [성별에 따른 맥박수의 평균계산]

tapply(survey$Pulse, INDEX= survey$Sex, FUN= mean, na.rm= TRUE)

# 두 개의 집단 변수를 모두 고려한 (지정할 시, 리스트 형식으로 지정)

(3) [운동습관별, 성별 평균 맥박수 구하기]

tapply(survey$Pulse, INDEX=list(survey$Exer, survey$Sex), FUN= mean, na.rm= TRUE)

- 두개의 집단변수가 교차표의 행과 열로 사용이 돼서, 셀값으로서 맥박수의 평균 출력
- 고차표 형식으로 집단별 통계량 계산
-> INDEX 인수에 집단을 나타내는 변수 두 개 지정

-> 행) 운동습관을 나타내는는 세개의 범주/ 열) 성별을 나타내는 두개의 범주
-> 해당 셀 값은 '두 범주의 조합에 따른 맥박수의 평균' (운동을 자주하는 여성: 맥박수의 평균이 73.6)

#aggregate()함수를 이용해도 출력형태는 다르지만, 동일한 결과를 얻을 수 있음

(1) [운동습관별 맥박수의 평균 계산]

aggregate(survey$Pulse, by= list(survey$Exer), FUN= mean, na.rm=TRUE)

- aggregate( , ): 첫번째 인수 -> 데이터셋 지정/
- aggregate( , ): 두번째 인수 (by 인수) -> by 인수에 리스트 형식으로 집단을 나타내는 변수 지정
- aggregate( , ): 세번째 인수 (FUN인수) -> 사용할 함수 지정

# 집단을 나타내는 변수 앞에 'Group.1'이라는 이름이 출력 -> 이름 지정도 가능

aggregate(survey$Pulse, by= list(Exercise= survey$Exer), FUN= mean, na.rm=TRUE)

(2) [운동습관별, 성별에 따른 맥박수 평균 산출]

#aggregate() 함수도 '두 개의 집단변수 지정 가능'

aggregate(survey$Pulse, by= list(Exercise=survey$Exer, Sex=survey$Sex), FUN= mean, na.rm=TRUE)

-> 운동습관과 성별이 각각의 열을 차지하면서, 두개의 변수의 범주 조합에 따른 맥박수 평균을 하나의 표로 출력
# aggregate() 함수는 데이터프레임 형식의 데이터셋을 처리할 수 있음 (tapply() 함수와 다른 점)
= 첫번째 인수 -> 한개의 변수만 지정할 수 있는 게 아닌, 두 개 이상의 변수를 지정해서 여러 개의 변수에 대한 집단별 기술통계량 한 번에 계산 가능

(3) [운동습관별 맥박수 평균 + 운동습관별 나이 평균]

# 데이터셋으로 두개의 변수 지정

aggregate(survey[c('Pulse','Age')],
          by= list(Exercise=survey$Exer), 
          FUN= mean, #fun 인수 = 사용자 정의 함수도 지정 가능능
          na.rm=TRUE)

-> 사용자 지정 함수

#사용자 지정 함수
myStats <- function(x, na.rm=FALSE) {
  if (na.rm) x <- x[!is.na(x)]
  n <- length(x)
  mean <- mean(x)
  sd <- sd(x)
  skew <- sum((x-mean)^3/sd^3)/n
  kurt <- sum((x-mean)^4/sd^4)/n - 3
  return(c(n=n, mean=mean, sd=sd, skewness= skew, kurotosis= kurt))
}

[FUN() 인수 이용]
aggregate(survey[c('Pulse','Age')],
          by= list(Exercise=survey$Exer), 
          FUN= myStats, #fun 인수 = 사용자 정의 함수도 지정 가능능
          na.rm=TRUE)

-> myStats() 함수에서 정의된 그런 톨계량 출력
-> 운동습관별, 맥박수에 대한 통계량/ 나이에 대한 통계량

5. [by()함수 이용- 집단별 기술통계량 계산]

- by(): 첫번째 인수 -> 데이터셋 지정
- by(): 두번째 인수 -> INDICES 인수의 집단별 변수 지정

by(survey[c('Pulse','Age')],
   INDICES= list(Exercise=survey$Exer), #운동습관 변수- 집단변수로 지정
   FUN= summary)

aggregate(survey[c('Pulse','Age')],
          by= list(Exercise=survey$Exer), 
          FUN= summary) #fun 인수 = 사용자 정의 함수도 지정 가능

-> by()와 aggregate()는 내용은 같지만, 형식은 다름

5-1. [by 함수의 FUN 인수에 사용자 지정 함수 지정]

by(survey[c('Pulse','Age')],
   INDICES= list(Exercise=survey$Exer), #운동습관 변수- 집단변수로 지정
   FUN= function(x) sapply(x, myStats, na.rm= TRUE)

-> FUN 인수에 사용자 정의 함수를 바로 지정할 수 없음, sapply()함수에 데이터값을 하나씩 넘겨줘서 처리하는 방식으로 지정
# function()함수를 호출해서 데이터셋에 지정되는 변수를 하나씩 지정
-> myStats()에서 정의한 함수들이, '운동습관의 세개 범주별'로 잘 출력됨

5-2. describeBy()

- describeBy()함수는 같은 패키지에 포함되어 있는 , describe()함수가 제공하는 것과 동일한 기술통계량을 집단별로 산출
# describeBy(): 첫번째 인수 -> 데이터셋 지정
# describeBy(): 두번째 인수(group 인수) -> 집단변수를 지정함

# describe()함수가 제공하는 기술통계량을 집단별로 구분함

describeBy(survey[c('Pulse','Age')],
           group = list(Exercise=survey$Exer))

자료 출처: https://www.youtube.com/watch?v=eF4Kl7xeJOI&list=PLY0OaF78qqGAxKX91WuRigHpwBU0C2SB_&index=5