| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 정기시험
- 데이터분석
- 기하분포
- 파이썬
- 3과목
- 절사평균
- 3ㅣ
- 데이터독학
- r #데이터분석 #adsp #자격증 #대외활동 #여름방학 #취업준비
- 오블완
- 데이터분석프로젝트
- WISET
- 방학
- 신청
- 옻
- 독학
- 대학생
- 베르누이
- 자격증
- R
- dsa프로젝트
- 기술통계
- ADSP
- 연속확률분포
- 인스타툰 #지식 #클래스101 #전자책 #인스타그램 #인스타 #만화 #웹툰 #아이패드드로잉
- 머신러닝
- 평균
- 티스토리챌린지
- 분위수
- 이항분포
- Today
- Total
mmings_pring_day
[통계 데이터분석] 분산분석- 일원분산분석 본문
1. 일원분산분석 (one-way ANOVA)
- 집단을 구분하는 독립변수가 한 개일 때 모집단 간 평균의 동일성 검정
- 귀무가설) 집단 간 평균은 모두 동일하다
- 대립가설) 집단 간 평균은 모두 동일하지 않다
(어느 한 집단이라도 다른 집단과 통계적으로 유의한 차이를 보인다면 귀무가설은 기각됨)
- InsectSprays 데이터셋 = 살출제에 대한 실험 데이터가 기록되어 있음
str(InsectSprays)
- > 여섯 종류의 살충제를 각각 12개의 실험 공간에 살포한 다음, 살아남은 해충의 개수를 기록했음
- spray 변수 = 살충제 종류 (A~F: 여섯 개의 살충제명이 포함되어 있음)
- count 변수= 해당 살충제를 살포한 다음 살아남은 해충의 개수 (갯수가 적을수록 좋은 것!)
* 각 살충제별로 12개 씩의 데이터가 수집되어 있어, '집단별 표본크기'는 12.
- tapply( )함수 = 집단별 표본 크기 계산
# tapply()함수의 첫번째 인수 = 대상 벡터 지정 (count 변수)
# tapply()함수의 두번째 인수 = 집단 변수 지정
# tapply()함수의 세번째 인수 = 집단별로 구분된 데이터에 적용할 함수 지정
# length() 함수 = 관측값의 개수 계산
tapply(InsectSprays$count, InsectSprays$spray, length)
# 각 살충제별 평균 계산
tapply(InsectSprays$count, InsectSprays$spray, mean) #일원분산분석
# 각 살충제별 표준편차 계산
tapply(InsectSprays$count, InsectSprays$spray, sd)
- length( ) 함수 = 관측값 개수 계산 (A부터 F 까지 여섯 개의 살충제 별로 12개 씩의 관측값 확인 가능!

-> 살충체별 '평균'과 '표준편차'에 있어서 차이가 큰 것을 볼 수 있었음
(예- *평균 살충제 C = 평균 2.08 가 살아남음, 살충제 F = 평균 16.67 마리가 살아남음 => 살충제별 살충효과의 차이가 큼
- plotmeans( ) 함수 = 집단별 평균과 평균에 대한 신뢰구간을 그래프상에 함께 보여줌
library(gplots)
windows(width=7.0, height=5.5)
# plotmeans()함수의 첫번째 인수(포뮬러 형식)= 종속변수(count)와 독립변수(spray)
# -> '종속변수' 살충제 살포 후에 살아남은 해충의 개수를 나타내는 count 변수 지정
# -> '독립변수' 집단을 나타내는 spray 변수 지정
# plotmeans()함수의 두번째 인수(data 인수)= 사용하고 있는 데이터셋 지정
plotmeans(count ~ spray, data=InsectSprays)
-> x 축: 여섯 개의 살충제가 배치되어 있음/ y축: 살아남은 해충의 개수
* 살충제 별로 평균을 중심으로 해서 '신뢰구간'이 함께 표현됨
-> plotmeans() 함수는 '기본적으로 95% 신뢰구간'을 보여줌 -> 신뢰구간의 확률을 바꾸고 싶으면, p 인수를 추가로 지정해서 확률을 바꿀 수 있음
* 95% 신뢰구간이 '어떤 살충제 간에는 서로 상당히 겹치고 있는 반면에, 다른 살충제와는 서로 겹치지 않음 *
-> 살충제 간의 평균의 차이가 존재하는 것처럼 보임!
# plotmeans()함수의 추가적인 인수 지정
# (1) barcol 인수 = 신뢰구간을 나타내는 막대의 색깔 지정
# (2) barwidth 인수 = 신뢰구간을 나타내는 막대의 두께 지정
# (3) col 인수 = 여섯 개의 살충제의 평균을 잇는 선들의 색깔 지정
# (4) lwd 인수 = 그 선의 두께 지정
# (5) xlab, ylab 인수 = x 축(spray 종류)과 y 축(살아남은 곤충의 개수)의 축 이름 지정
# (6) main 인수 = 그래프의 제목 지정
plotmeans(count ~ spray, data=InsectSprays,
barcol="tomato", barwidth=5, col="cornflowerblue", lwd=2,
xlab="Type of Sprays", ylab="Insect Count",
main="Performance of Insect Sprays")
- 상자도표_ boxplot( ) 함수 = 집단 간의 차이를 살펴볼 수 있는 그래프
-> 각 살충제별로 '중위수'나 '첫번째 및 세번째 사분위수'라던가, '이상점'과 같은 추가적인 정보 확인 가능!
# bowplot() 함수의 첫번째 인수(포뮬러 형식)= 종속변수와 독립변수 지정
# bowplot() 함수의 두번째 인수= 데이터셋 지정
# bowplot() 함수의 추가적인 인수 지정
# (1) col 인수= 상자의 색깔 지정
# (2) xlab, ylab 인수= x축(살충제의 종류), y축(살아남은 해충의 개수) 제목 지정
boxplot(count ~ spray, data=InsectSprays, col="tomato",
xlab="Type of Sprays", ylab="Insect Count",
main="Performance of Insect Sprays") #동그라미: 이상치
- 상자도표 상자의 하단부) 첫번째 사분위수를 나타냄/ 상단부) 세번쨰 사분위수를 나타냄
- > 관측값을 크기순으로 작은 값에서 큰 값으로 배열했을 때, 처음 25%에 해당하는 값(첫번째 사분위수), 75%(세번째 사분위수)
- 상자의 길이 = 사분위 범위를 의미함
- 상자 가운데 굵은 선 = 중위수를 나타냄
- 상자의 상단과 하단으로부터 뻗어 나오는 선의 끝은, 상자길이의 1.5배 범위 내에서의 최솟값과 최댓값을 나타냄
- 상자 길이의 1.5 배를 벗어나는 값) 이상적으로 정의됨 *상자도표 상에서 작은 동그라미로 표시됨 *
- 상자도표와 평균도표 (plotmeans) 를 바탕으로 생각: 여섯 개의 살충제 간의 살충효과가 동일하다고 보기 어려움
-> 상자도표) 분포들이 서로 많이 다르고, 중위수가 상당히 차이가 있음
[일원분산분석 -> 살충제 간 살충효과의 평균이 동일한지 통계적으로 검정]
- aov( ) 함수 = 일원분산분석 수행 함수
#반드시! 등분산성을 가정할 때만 사용할 수 있음
# aov()함수의 첫번째 인수(포뮬러 형식)= 종속변수(검정하고자 하는 count 변수) ~ 독립변수(집단) 지정
# aov()함수의 두번째 인수= 데이터셋 지정
# 일워분산분석 결과를 'sprays.aov'변수에 저장
sprays.aov <- aov(count ~ spray, data=InsectSprays)
sprays.aov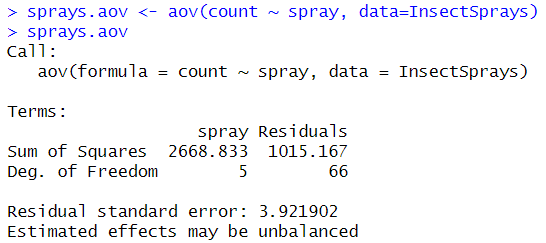
-> 가설검정을 위한 충분한 정보를 제공하지는 앉음
-> 분산분석을 수행해서 생성된 모델 객체에 summary( ) 함수를 적용해서 '충분한 정보' 파악 가능!
- summary( ) 함수의 분산분석 결과
# summary() 함수의 첫번째 인수= 분산분석 결과에서 생성된 모델 객체 지정
summary(sprays.aov) #분산분석표 추출
- spray 행 = 집단 간의 차이를 설명함/ Residuals 행 = 집단 내의 차이를 나타냄
- Df (자유도), Sum Sq (제곱합), Mean Sq (제곱합을 자유도로 나눈 분산)
- Mean Sq + Spray 행이 만나는 곳의 셀 값 = 집단 간 분산
- Mean Sq + Residuals 행이 만나는 곳의 셀 값 = 집단 내 분산
- F value= F 값/ F 값 이상이 발생할 확률 = Pr 열에 존재함
* 유의수준 0.05/ 0.01 에 비해서 매우 작은 Pr 값이기 때문에 '귀무가설 기각' (대립= 살충제 별 살충효과 차이가 있다) *
* 확률이 작다 = 모집단에서 '여섯 개 살충제 간에 살충효과의 평균이 같다'는 가정 하에서 표본으로부터 이렇게 큰 F 값을 관측할 확률이 너무 작기 때문에, 모집단에서 '여섯 개 살충제 간에 살충효과의 평균이 같다'는 가정을 받아들이기 어렵기에 귀무가설 기각/ 대립가설 채택 *
-> 하지만, 이것만으로는 '모집단 평균이 모두 동일하다는 주장을 기각할 수 있을 뿐이지, 어느 집단과 어느 집단이 서로 달라서 이러한 결과가 나왔는지는 알 수 없음
[다중비교]- model.table( ) 함수 = 개별 집단 간 평균의 차이를 확인할 수 있고, 구체적으로 어느 집단과 어느 집단의 평균값이 다를 가능성이 높은지를 확인 가능!
# model.tables() 함수의 첫번째 인수= 분산분석 모델 객체 지정
# model.tables() 함수의 두번째 인수(type 인수)
# -> model.tables()함수는 type 인수에 지정되는 값에 따라서 '집단 간 평균'의 차이를 두 가지 다른 형식으로 보여줌
# -> 'type= mean' = 전체평균과 함께 각 집단의 평균 확인
# -> 'type= effects' = 집단별로 각 집단평균과 전체평균의 차이를 볼 수 있음
model.tables(sprays.aov, type="means")
model.tables(sprays.aov, type="effects")

- 'type= "means"' => 여섯 개의 살충제 별로 평균값 확인 가능
- 'type= "effects"'
(예- 살충제 C 가 살포된 실험 공간에서는 전체 평균보다 7.4 마리 더 적은 해충이 생존해서 '살충제 C 의 살충효과가 가장 좋은 것'으로 확인!
살충제 F 는 전체 평균보다 '7.2' 마리 더 많이 생존해서 살충효과가 가장 미흡함!)
-> 분산분석 결과) 대립가설 채택 (살충제 간에 살충효과의 차이가 있다)
= 추가로 이러한 개별 집단 간 차이의 유의성을 통계적으로 검정하는 것이 때론 유용함
-> why: 개별 집단 간에 '의미있는 차이가 존재하는지 여부'는, 우리가 어떤 집단을 선택할 때 영향을 미칠 수 있기 때문임.
(예- 살충제를 구매하는 결정을 해야 할 때, 가장 살충효과가 좋은 살충제 C 를 사는 것이 반드시 좋은 결정은 아닐 수 있음.
살충제 C 의 경우엔, 살충효과는 당연히 가장 좋겠지만, 아무래도 가격이 가장 비쌀 것이기 때문에!
만일 살충제 C 와 살충제 D 의 살충효과가 유사한데 살충효과 D 의 가격이 훨씬 저렴하다면, 살충제 D 를 사는 것이 효율적임)
- 살충제 D 와 살충제 C, 이 두 살충제 간의 살충효과에 있어서 '정말 통계적으로 유의미한 차이가 있는지' 검정 => 터키HSD 검정 이용
[사후분석] 다중비교를 통한 집단 간의 차이 검정
- TurkeyHSD( )함수 = 리스트 형식의 모델 객체 생성 -> 독립변수 이름을 원소의 이름으로 사용해서
(생성된 모델 객체는 '리스트 구조')
# TukeyHSD()함수의 인수 지정= 분산분석 모델 객체 지정
sprays.compare <- TukeyHSD(sprays.aov)
sprays.compare
-> 이 객체) 여섯 종류의 살충제가 만들어내는 '모든 가능한 비교 쌍의 평균 차이'를 보여주는 열을 갖고 있음
-> 평균차이에 대한 95% 신뢰구간의 하한값(lwr 열) 과 상한값(upr 열)을 보여주는 열을 포함하고 있음
-> [p adj 열] : 평균차이에 대한 p 값이 포함되어 있음
(유의한 차이가 나타나면 => 분산분석에서는 '모든 살충제 간의 살충효과가 동일하다'는 귀무가설을 기각함)
-> 살충제 D 와 살충제 C 의 비교쌍을 보면) 맨 끝에 유의확률이 '0.49'로써, 0.05 를 기준으로 봤을 때, 통계적으로 유의하지 X
(= '살충제 D 와 살충제 C의 살충효과의 차이는 통계적으로 의미가 없다' 귀무가설 채택)

-> 모든 비교쌍 간의 정보는 '리스트 구조'의 spray 원소 내에 다시 형렬 형식으로 들어가 있음
-> 특정 비교쌍을 추출하기 위해선, 일반적인 리스트의 '원소 추출 방식'과 그 안에 포함되어 있는 '행렬을 추출하는 방식' 이 두가지를 이용해서 추출 가능!
(예- 살충제 D 와 살충제 C 에 대한 '평균 비교 분석 결과'만을 추출하기 위해선, 인덱싱 사용
# sprays.compare$spray= 리스트 구조로부터 spray 원소 내의 값을 추출
# -> 안이 행렬이기 때문에 '행렬 인덱싱'을 이용해서 다시 추출!
sprays.compare$spray['D-C',]-> 살충제 D 와 살충제 C 의 분석 결과만을 추출 가능

-> 살충제 D와 살충제 C 간의 평균 차이에 대한 p 값은 '0.49'로서 유의수준 0.05 에 비해 매우 크기 때문에 귀무가설 채택
(두 살충제 간의 살충효과 차이가 없다)
-> 살충제 D 가 살충제 C 에 비해서 값이 많이 쌀 경우 -> '살충제 D 구매'가 충분함
- plot( )함수 = 집단 간의 차이
windows(width=7.0, height=5.5)
# plot()함수의 인수 = TukeyHSD() 함수로부터 생성된 모델 객체 지정
plot(sprays.compare)
# plot()함수의 추가적인 인수 지정
# (1) col 인수 = 신뢰구간에 선의 색상 지정
# (2) 'las=1' => Y축의 축과 평행으로 되어 있는 '비교쌍들의 글씨'가 축과 평행으로 되어 있어서,
# 90도로 돌려서 'x축'과 평행하도록 만들어서, 글자를 더 읽기 쉽도록!
plot(TukeyHSD(sprays.aov), col="blue", las=1)
#0에 걸쳐있음 -> 통계적으로 살충효과 차이가 없음!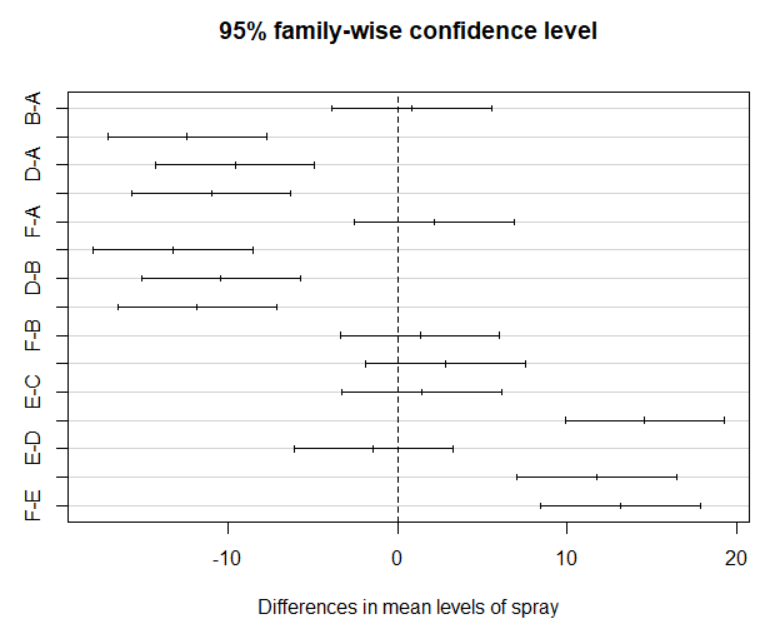

-> 가로선 (집단 간 평균의 차이에 대한 95% 신뢰구간)
* 신뢰구간이 0을 포함하지 않으면, 집단 간 차이는 통계적으로 유의하다는 것을 나타냄
신뢰구간 내에 0이 포함되어 있으면, 두 집단 간의 차이는 의미가 없다 = 0일 수도 있다 = 두 집단 간의 평균은 같을 수도 있다*
-> 살충제 D 와 살충제 C의 비교쌍을 보면, 신뢰구간 내에 0이 포함되어 있음 = 두 살충제 간의 살충효과는 차이가 없다
- multcomp 패키지 이용 = 다중비교 결과를 다른 방식으로 표현!
-> 터키HSD 검정을 수행하고, 그 결과를 상자도표 형태의 그래프로 나타내보기
- glht( ) 함수 = 터키HSD 검정 수행
windows(width=7.0, height=5.5)
library(multcomp)
# glht()함수의 첫번째 인수(model인수)= 분석을 위한 모델 객체 지정
# glht()함수의 두번째 인수(linfct인수)= 검정할 가설 지정
# -> spray 변수에 의해 구분되는 집단을 바탕으로 터키HSD 다중비교를 수행하는 모델 지정 (mcp 함수이용)
tuk.hsd <- glht(model=sprays.aov, linfct=mcp(spray="Tukey"))
# cld()함수의 첫번째 인수= glht()함수로부터 만들어진 모델 객체 지정
# glht()함수의 두번째 인수(linfct인수)= 검정할 가설 지정
cld(tuk.hsd, level=0.05)
plot(cld(tuk.hsd, level=0.05), col="orange", las=1)-> 이 결과, 객체로부터 모든 범주 쌍의 비교 결과를 cld( ) 함수를 이용해서 '알파벳 문자'로 추출 가능!

-> 여섯 개의 살충제 별로 대응되는 알파벳 문자가 출력되는 것을 확인 가능!
-> 같은 문자를 공유하는 살충제는 '서로 평균이 다르지 않다'는 것을 나타냄!
-> 알파벳 b 를 공유하고 있는 '살충제 A, B, F는 서로 평균이 같다'
-> 알파벳 a 를 공유하고 있는 '살충제 C, D, E'역시 서로 평균이 같다'
-plot( ) 함수 = 그래프 형태로 표현 가능
-> 상자도표의 각 상자는 범주를 나타냄 *여섯 개의 살충제 종류를 의미함 *
-> 상자 상단_ 알파벳 문자가 표시되어 있음 (같은 문자를 공유하는 범주는 서로 평균이 같다는 것을 의미함)
* 특히, 범주의 개수가 많을 경우- 유용하게 사용 가능! *
* 그래프- 각 범주별로 '종속변수 값의 분포를 볼 수 있다'는 장점 제공!
2. 분산분석 가정 (관측값의 조건)
- 정규성: 종속변수는 정규분포를 함
- 등분산성: 각 집단의 분포는 모두 동일한 분산을 가짐
-> 분산분석을 수행하기 위해서, 두 가지 조건을 완벽하게 충족해야 되는 것은 아니지만, 이 조건을 충족하면 '보다 신뢰할 수 있는 결과'를 얻을 수 있음!
'통계' 카테고리의 다른 글
| [통계 데이터분석] 공분산분석, 반복측정 분산분석, 다변량 분산분석 (0) | 2024.10.17 |
|---|---|
| [통계 데이터분석] 분산분석- 이원분산분석 (0) | 2024.10.17 |
| [통계 데이터] 분산분석 가정 (0) | 2024.10.14 |
| [통계 데이터분석] 분산분석- F 검정 (1) | 2024.10.13 |
| [통계 데이터 분석] 분산분석 (분산분석 설계) (0) | 2024.10.11 |




