| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 독학
- r #데이터분석 #adsp #자격증 #대외활동 #여름방학 #취업준비
- 머신러닝
- ADSP
- 평균
- 기술통계
- 데이터독학
- 베르누이
- 데이터분석
- 인스타툰 #지식 #클래스101 #전자책 #인스타그램 #인스타 #만화 #웹툰 #아이패드드로잉
- 데이터분석프로젝트
- 3ㅣ
- 3과목
- 절사평균
- 신청
- R
- 자격증
- 파이썬
- 대학생
- 이항분포
- 티스토리챌린지
- 오블완
- 연속확률분포
- 옻
- WISET
- 정기시험
- 분위수
- dsa프로젝트
- 기하분포
- 방학
- Today
- Total
mmings_pring_day
[통계 데이터 분석] 분산분석 (분산분석 설계) 본문
0. 분산 분석
✅ t 검정을 이용한 평균 검정을 수행하면 두 개의 표본을 바탕으로 해서 , 각각 대응되는 두 개의 모집단 평균이 서로 동일한 지 검정 가능 -> 두 개의 집단이 있을 때 '그 두 집단의 평균값이 같은지'를 검정 가능
✅ t 검정을 이용해서 두 개를 초과하는 집단 (예- 새 개 집단 간의 평균값이 같은지는 검정 불가!)
- 여러 모집단 간의 평균의 동일성을 검정 [분산분석]
(분석의 목적이나 설계 방식에 따라 분산 분석의 종류가 나뉨)
* 계절별 아이스크림 판매량/ 혈액형별 영화 선호도 등 (둘 이상의 집단 간의 평균의 동일성 검정)
1. 일원분산 분석
- 일원분산분석 (one-way ANOVA)
: 집단을 구분하는 범주형 변수가 한 개인 경우 = 집단이 하나 (일원)
* (( 집단이 하나인데, 그 안에 범주 는 3 개인 경우 (둘 이상) )) *

실험설계) 집단을 구분하는 하나의 범주형 변수만 갖고 있기 때문에 '일원분산 분석'
1-1. 집단 간 일원분산분석
- [집단 간 일원분산분석] 각 환자의 치료효과는 둘 중에 한 가지인 '심리치료' 방법에 대해서만 측정
- 범주형 변수: 심리치료 방법 (첫 번째 심리치료 방법: A/ 두 번째 심리치료 방법: B) -> 집단이 두 개임!
- 독립변수: 심리치료 -> 종속변수: ADHD 평가 점수

[분산분석의 목적]
: 독립변수인 심리치료 방법이 종속변수인 ADHD 평가점수에 영향을 미치는지를 검정하는 것
-> 심리치료 방법에 따라서 ADHD 평가점수가 다른지를 보기 위함
[실험 방법]
(집단 간 요인: 치료 방법_ 범주형 변수의 요인으로서의 역할 확인): 10 명의 실험 참여자를 모집한 다음에 이들 가운데 무작위로 선정한 반은 4주 동안에 심리치료 A 를 시행하고, 나머지 반에 대해서는 4주 동안에 심리치료 B 를 시행함 -> 4주의 치료 기간이 종료된 다음에 참가자의 ADHD 점수 측정
* 환자는 심리치료 방법에 따라 구분되는 두 집단 가운데 하나에만 할당되고 어떤 환자에게도 두가지 심리치료를 모두 시행하지 않음 *
[가설 검정 방법: F 검정]
: F 검정 결과가 통계적으로 유의하면 '두 심리치료 방법에 따른 효과'는 다르다는 결론을 내릴 수 있음
1-2. 집단 내 일원분산분석
* 집단을 구분하는 하나의 범주형 변수만 존재하기 때문에 역시 일원분산분석 *
- [집단 내 일원분산분석] 심리치료의 '치료 기간' 경과 후의 '치료효과'에 대해서만 측정
: ( 각 환자의 치료효과는 기간 변수 내의 두 범주 모두에 대해서 측정)
- 범주형 변수: 치료 기간 (4주와 16주 두 개의 범주를 갖음) => (('기간'에 따른 변화 (기간-> 일원)
-> 각 실험 참여자에 대해 반복해서 측정이 이루어지고 있기 때문에 -> '반복측정 분산분석' 이라고도 함 (ANOVA)
- 독립변수: 치료 기간 -> 종속 변수: ADHD 평가 점수

[실험 방법]
(집단 내 요인: 치료 기간 변수_ 범주형 변수의 요인으로서의 역할 확인
: 10 명의 실험 참여자 모두에게 4주 동안에 심리치료 A 를 처치하고 ADHD 평가점수를 기록함 -> 16주 후에 다시 ADHD 평가점수를 측정해서 기록함
* 환자는 기간에 따라 구분되는 두 집단 모두에 할당됨 -> 동일한 환자에 대해서 기간의 두 가지 범주에 따른 두 개의 측정값이 기록됨 *
[가설 검정 방법: F 검정]
: F 검정 결과가 통계적으로 유의하면 '환자의 치료효과는 진료를 종료한 시점인 4주 시점과 그 이후 16주가 지난 시점 사이에서 변화가 있었다'는 다르다는 결론을 내릴 수 있음
=> 이와 같은 두 가지의 실험설계를 결합하면
'심리치료 방법에 의한 치료효과의 차이'와 '기간에 따른 치료효과의 차이'를 모두 동시 검정 가능!
2. 이원분산 분석

- 이원분산분석 (two-way ANOVA)
: 집단을 구분하는 범주형 변수가 두 개인 경우
-> 각 실험 참여자에 대해서 반복해서 두 번 측정이 이루어지고 있기 때문에 '반복측정 분산분석' (ANOVA)
- 주효과 : 심리치료 방법의 영향, 기간의 영향 (두 개의 범주형 변수에 대응되는 영향)
= 집단을 구분하는 변수가 치료효과에 미치는 영향 -> 각각의 변수가 미치는 영향으로 '일워분산분석'을 통해 알 수 있음
- 상호작용 효과: 심리치료 방법과 기간 간 상호작용의 영향
(두 개의 범주형 변수가 서로 부딪혀서 만들어지는 심리치료 방법과 기간 간 상호작용의 영향)
= 두 개의 변수가 만났을 때 결과가 달라지는지 (예- 다이어트 약과 성별에 따른 변화 분석)
- 독립변수: 심리치료 방법, 기간 -> 종속 변수: ADHD 평가 점수
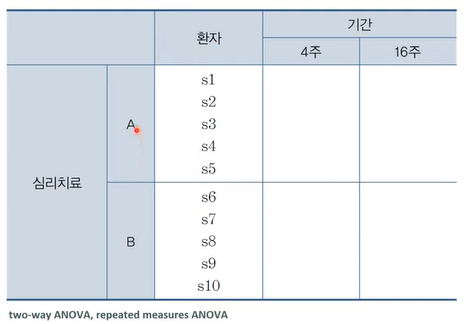
- 집단 구분 변수 (기간, 심리치료_두 개) => 이원분산분석
- 심리치료 A 를 받으면서 기간이 4주가 지난 집단
- 심리치료 A 를 받으면서 기간이 16주가 지난 집단
- 심리치료 B 를 받으면서 기간이 4주가 지난 집단
- 심리치료 B 를 받으면서 기간이 16주가 지난 집단
[실험방법]
: 10명의 실험 참여자 가운데 다섯 명은 심리치료 방법 A 에 할당하고 나머지 다섯 명은 심리치료 방법 B 에 할당
-> 치료 종료 시점인 4주 후에 ADHD 평가점수를 측정하고, 이어서 16 주 후에 다시 ADHD 평가점수를 측정함
[가설 검정 방법: 세 개의 F 검정이 필요함]
: 주효과 두 개와 상호작용효과 한 개에 대한 각각의 F 검정을 수행함
- 심리치료에 대한 F검정 결과가 통계적으로 유의
-> '심리치료 A 와 심리치료 B 의 ADHD 치료효과가 다르다'는 것을 나타냄
- 기간에 대한 F 검정 결과가 통계적으로 유의
-> ' ADHD 평가점수가 4주 시점 이후부터 16주 시점까지 변화했다'는 것을 의미함
- 심리치료 방법과 기간 간의 상호작용에 대한 F 검정 결과가 통계적으로 유의
-> '두 ADHD 심리치료 방법은 기간에 따라 다른 치료효과를 보인다는 것' 을 나타냄
(4주 시점과 16주 시점 간의 ADHD 평가점수의 변화 차이는 심리치료 방법에 따라서 다르게 나타난다는 것을 의미함)
=> 심리치료 방법과 기간 모두를 포함함으로써 'ADHD 치료효과에 대한 심리치료 방법의 영향과 기간의 영향, 그리고 심리치료 방법과 기간 간 상호작용의 영향을 파악 가능'
공분산분석, 다변량 분산분석, 다변량 공분산분석
3-1. 공분산분석
- 공분산분석 (analysis of covariance , ANCOVA) : 공변량을 통제하여 독립변수의 순수한 영향을 검정
- 스트레스 지수: 공변량 (환자가 가진 내재적인 특성)
독립변수에게 영향을 끼칠 수 있는 공변량 (이를 제거하여 순수한 영향을 검정함)
= ADHD 는 스트레스와 밀접한 관련이 있을 수 있음
* (실험설계에서 실험 참여자들을 두 가지 심리치료 방법에 무작위로 할당하기는 했지만, 두 심리치료 집단에 포함된 실험 참여자들의 스트레스 수준은 각각 다를 수 있음)= 분산분석의 결과에 의해서, '심리치료 방법에 따라서 ADHD 치료효과의 차이가 있다' 라는 결론을 얻었을 때,
그 ADHD 치료효과의 차이가 심리치료 방법 때문만이 아니라 '실험 참여자의 스트레스 수준 차이에 영향을 받았을지도 모름'
= 실험 참여자의 스트레스 수준을 사전에 측정하여, 그 측정 데이터를 갖고 있다면 실험 참여자의 스트레스 수준을 통제해서 '심리치료 방법에 따른 순수한 차이 검정 가능'
3-2. 다변량 분산분석
- 다변량 분산분석 (MANOVA0
: 두 개 이상의 종속변수를 포함
ADHD 를 측정하기 위한 종속변수로서, ADHD 평가점수 한 개만을 사용했음.
하지만, 연구의 타당성을 높이기 위해서 측정 지표를 추가할 수 있음.
(예- 브라운 주의력결핍장애 평가점수 혹은 코너스부모/ 교사 평가점수 와 같은 지표 )
3-2 (1) . 다변량 공분산분석
- 다변량 공분산분석 (MANCOVA)
: 두 개 이상의 종속변수와 공변량 포함
'통계' 카테고리의 다른 글
| [통계 데이터] 분산분석 가정 (0) | 2024.10.14 |
|---|---|
| [통계 데이터분석] 분산분석- F 검정 (1) | 2024.10.13 |
| [통계 데이터 분석] 평균검정 (t 검정) (0) | 2024.10.06 |
| [통계 데이터 분석] 가설검정과 확률분포 ⭕ (0) | 2024.09.29 |
| [통계 데이터분석] 데이터 요약- 연속형 변수 ⭕ (0) | 2024.09.29 |




