| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- r #데이터분석 #adsp #자격증 #대외활동 #여름방학 #취업준비
- ADSP
- 이항분포
- 독학
- 신청
- 연속확률분포
- 기술통계
- 인스타툰 #지식 #클래스101 #전자책 #인스타그램 #인스타 #만화 #웹툰 #아이패드드로잉
- WISET
- 오블완
- 베르누이
- 절사평균
- dsa프로젝트
- 티스토리챌린지
- 기하분포
- 데이터독학
- R
- 평균
- 파이썬
- 대학생
- 데이터분석
- 데이터분석프로젝트
- 옻
- 분위수
- 정기시험
- 머신러닝
- 자격증
- 3ㅣ
- 방학
- 3과목
- Today
- Total
mmings_pring_day
[통계 데이터분석] 더미변수 회귀분석/ 매개효과/ 조절효과 본문
회귀분석- 더미변수 회귀분석
- 독립변수 (연속형 변수) : 교육기간/ 자동차 모델- 마력, 무게 (다중회귀분석) 등등
- 독립변수가 범주형 변수일 때 독립변수를 더미변수로 변환하여 회귀분석 수행
- 더미변수란 어떤 속성 (또는 사건)이 존재할 경우 그 값을 1로, 존재하지 않을 경우 그 값을 0으로 코딩한 인위적 변수
- 더비변수를 이용한 회귀분석을 통해 얻ㄱ 되는 회귀계수는 1로 코딩된
소득 = Bo + B1 X 성별더미
- 독립변수 성별더미: 남자는 1, 여자는 0으로 코딩
(0으로 코딩된 소득은 '절편')
- 회귀계수 B1: 코드값이 1인 범주 (즉, 남자)의 소득에 대한 영향
(0으로 코딩된 범주와 1로 코딩된 범주의 종속변수 간의 간격)
범주가 여러 개일 경우) 확장편
[더미변수 코딩과 회귀식]

- 계절변수가 연속형 변수가 아니기 때문에 = Bo + B1 X 계절 (X)
- 범주의 개수가 4개인 경우: 더미변수가 3개가 됨 -> 기준 범주를 만들면 가능함!
(기준 범주: 해석이 용이한 범주로 설정하면 됨)
=> 봄: Bo / 여름: Bo + B1 X D1(1) / 가을: Bo + B2 X D2(1) / 겨울: Bo + B3 X D2(1)
=> B1/ B2/ B3: 기준 범주와 해당 범주 간의 종속변수값 차이
- B1: ( 봄: Bo) - (여름: Bo + B1)
- B2: (여름: Bo + B1) - (가을: Bo + B2)
- B3: (가을: Bo + B2)- (겨울: Bo + B3)
-
-
str(InsectSprays)
levels(InsectSprays$spray)- 살충제 (독립변수) , 살아남은 회충의 개수 (연속형 변수)
-> 독립변수를 더미변수로!

tapply(InsectSprays$count, InsectSprays$spray, mean)
- lm( ) 함수: 자동으로 더미범주화 시키는 함수
sprays.lm <- lm(count ~ spray, data=InsectSprays)
summary(sprays.lm)
sprays.lm <- lm(count ~ spray, data=InsectSprays)
summary(sprays.lm)
- 14.5) 기준 범주인 '스프레이 A '를 뿌렸을 때 살아남은 해충 개수 (절편)
-> 예측하고자 하는 종속 변수: 살아남은 해충의 개수 : count
-> 독립변수: 살충제의 종류
contrasts(InsectSprays$spray)
- 총 살아남은 해충 개수= 14.5 + 스프레이B*0.83 + 스프레이C*(-12.4) + 스프레이D*(-9.6) + 스프레이E*(-11) + 스프레이F*2.2
- 스프레이 C 를 뿌렸을 때 살아남은 해충 개수(살충효과): 14.5 + 1 * (- 12.42) = 2.083
-
[분산분석과 동일함: 집단 간의 차이]

-> 스프레이 C,D,E: 통계적으로 유의하다는 것 (통계적으로 유의한 차이가 있다) = 모집단에서 0일 수가 없다 (기준 범주와 명확한 차이가 있다)
-> 통계적으로 유의하지 않음= 모집단에서 0일 수도 있음 = 기준 범주와 종속변수 간의 차이: 살충효과의 차이가 없다
- aov( ) 함수: 분산분석 진행하는 함수 (일원분산분석)
- TukeyHSD( ) 함수: 사후분석
sprays.aov <- aov(count ~ spray, data=InsectSprays)
summary(sprays.aov)
TukeyHSD(sprays.aov)
- 기준범수 결정하기 (스프레이 F) -> 해석이 용이한 범주
-> 모든 더미변수가 값이 0일 때, 절편: 스프레이 F 에 의해 설정됨
- relevel( ) 함수: 기준범주 설정하는 함수
respray <- relevel(InsectSprays$spray, ref=6)
sprays.lm <- lm(count ~ respray, data=InsectSprays)
summary(sprays.lm)
contrasts(relevel(InsectSprays$spray, ref="F"))

- 기준범주 를 중심으로 두고 해석: 기준범주 대비 나머지 범주들의 유의성 검정? (종속변수 값의 차이)
- 기준범주 = 해석이 용이한 범주
회귀분석- 매개효과분석 (직접적인 관계가 아니라, 간접적인 영향을 미치는 관계)
- 예) 소득이 높으면 -> 기대수명 증가
=> 소득이 높음 -> 좋은 의료환경 -> 기대수명 증가 (합리적) : 간접적 영향 관계
- 첫번째 변수 X 가 두번째 변수 M 에 영향을 미치고, 이이서 차례로 그 변수가 다시 세 번째 변수 Y 에 영향을 미치는 연쇄적인 영향관계를 검정 (간접효과)
- 두 변수 X 와 Y 사이에서 일련의 영향관계가 어떠한 과정을 거쳐 발생하는지 설명하는 변수 M 을 매개변수라고 함
매개효과모델

[총효과모델]
- c : X의 회귀계수
[매개효과모델]
- X -> M : a 라는 회귀계수
- M -> Y: b 라는 회귀계수
- (M 이 포함되어 있을 때) X -> Y: c' 라는 회귀계수 (M 을 통제한 상태에서)
[c 의 분류]
- 총효과: 직접효과 + 간접효과
-> 총효과(c) : 직접효과: c' + 간접효과: ab
if 매개효과가 존재할 시) 총효과모델에서의 c > 매개효과모델에서의 c' (부분매개)
if c' = 0 ) 총효과(c) = 간접효과 (ab) => 완전히 매개변수에 의존하게 됨 (완전매개)
바론 & 케니 매개효과분석

1) 매개 변수 없이, 독립변수와 종속 변수 만의 관계로 모델 형성 (단순회귀분석)
-> 총효과 확인 (X -> Y 영향을 미치는지)
if 유의하지 않으면, 소득이 기대수명에 영향을 안 미침 (아예 관계가 없음: 매개효과도 존재하지 않을 것 ?)
2) 매개변수 O , 종속변수 X
-> 매개변수 (M)가 새로운 종속변수 가 됨
* 매개효과가 존재한다고 하면, a 회귀계수가 통계적으로 유의해야 함!!! (확인)
-> X 가 M 에 영향을 미칠 때, M 의 매개효과가 의미가 있음!
3) 독립변수 (X), 매개변수(M), 종속변수 (Y)
- X-> Y: 직접효과( c')
- M -> Y: b 회귀계수
* 매개효과가 존재한다고 하면, b 가 통계적으로 유의해야 함 (b 가 통계적으로 유의한 지 확인!)
* 종속변수 Y 에 대한 독립변수 X 의 회귀계수 c' 은 사라지거나 적어도 약화되어야 함 (사라지면 = 통계적으로 유의하지 않으면, M 은 Y 와 X 사이를 완전 매개한다고 얘기함)
=> a, b 가 0이 아니면,
4) c' 이 통계적으로 유의한지, 아닌지 확인 / c 보다 작은지 확인
- c > c' ) 간접효과 O ,직접효과 O (부분매개)
- c' = 0) 완전매개 (실제 0이거나, 통계적으로 유의히지 않을 때)

- 배기량 이 높으면, 연비가 떨어짐
[검증하고픈 내용: 무게의 영향: 간접효과]
- 배기량이 높으면 -> 무게가 증가함 -> 연비가 떨어짐 : 무게에 매개효과가 존재하는지
1) 배기량 (disp) -> 연비 (mpg)
2) 배기량 (disp) -> 무게 (wt)
3) 무게 (wt) -> 연비 (mpg) (무게의 영향 이 통계적으로 유의한지)
소벨 검정: 매개효과의 유의성 검정

str(mtcars)
model.total <- lm(mpg ~ disp, data=mtcars)
summary(model.total)
-> p- 값 < 유의수준: 통계적으로 유의함 (배기량이 연비에 영향을 미침)
-> 배기량이 연비에 미친 총 효과는 '회귀계수 (-0.041215) 정도'
2) 무게의 영향
model.M <- lm(wt ~ disp, data=mtcars)
summary(model.M)
-> 매개변수 (wt) 와 독립변수 (disp) 와의 관계 검증: 유의미한 영향을 미치는 것을 확인!
3) 무게와 연비의 관계
= 독립변수를 통제한 상태에서, 매개변수와 종속변수 간의 영향 관계 검증
model.Y <- lm(mpg ~ disp + wt, data=mtcars)
summary(model.Y)
-> wt 의 영향이 통계적으로 유의함 (완전매개)
-> 매개효과모델에서, 모집단에서 배기량과 연비 간의 직접효과가 사라짐!
-> 총효과모델에선, 배기량과 연비 관계가 유의미했는데 (총효과 존재함)/
'무게' 라는 매개변수에 의해서 배기량과 연비 간의 직접효과가 사라짐 (자동차 무게는 배기량과 연비 간의 관계를 완전매개함)
=> 간접효과 산출 (ab) = 0.007 * (-3.351)
- sobel( ) 함수 = 간접효과의 통계적 유의성 검정 하는 함수
library(multilevel)
# sobel() 함수의 1. 인수= pred 인수 (독립변수 지정)
# sobel() 함수의 2. 인수= med 인수 (매개변수 지정)
# sobel() 함수의 3. 인수= out 인수 (종속변수 지정)
model.sob <- sobel(pred=mtcars$disp, med=mtcars$wt, out=mtcars$mpg)
model.sob
- z.value: 통계적으로 유의성 검정
- pnom( ) 함수: 유의확률을 알 수 있는 함수
pnorm(abs(model.sob$z.value), lower.tail=FALSE)*2
-> p-값 < 유의수준 = 유의한 값을 가짐
-> 매개효과가 존재한다고 말할 수 있음
- mediation.test( ) 함수: 유의확률과 z- 값이 값이 나오는 함수
library(bda)
# mediation.test() 함수의 1.인수 = (mv 인수) 매개변수 지정
# mediation.test() 함수의 2.인수 = (iv 인수) 독립변수 지정
# mediation.test() 함수의 3.인수 = (dv 인수) 종속변수 지정
mediation.test(mv=mtcars$wt, iv=mtcars$disp, dv=mtcars$mpg)
- mediation 패키지의 mediate( ) 함수 이용하여 통계적 유의성 검정
library(mediation)
set.seed(123)
model.M <- lm(wt ~ disp, data=mtcars)
model.Y <- lm(mpg ~ disp + wt, data=mtcars)
model.mediation <- mediate(model.m=model.M, model.y=model.Y,
treat="disp", mediator="wt", boot=TRUE, sims=500)
summary(model.mediation)
- ACME (간접효과 = 매개효과)
- ADE (직접효과)
- Total Effect (총효과)
windows(width=7.0, height=5.5)
plot(model.mediation, cex=1.2, col="royalblue", lwd=2,
main="Mediation Effect Analysis")
조절효과분석
- 변수 X 와 변수 Y 간 관계에 대한 제 3의 변수 Z의 영향을 검정 (개입)
- 이때 제 3의 변수가 언제 어떤 조건 하에서 두 변수 간 관계에 영향을 미치는지 검정하며, 변수 Z 를 조절변수라고 함
예) 콜레스테롤 수치를 낮추는 약 -> 효과, 개입변수: 성별의 개입
- 조절변수는 두 변수 간의 관계를 강화시킬 수도 있고 약화시킬 수도 있으며, 때로는 관계의 방향을 바꿀 수도 있음

- 독립변수 (시험의 중요도) -> 종속변수 (시험에 따른 불안감) / 자신감 (조절변수)
=> 자신감이 높은 수험생, 불안감이 증가하는 속도가 낮음 (자신감이 낮은 수험생에 비해서)
조절효과모델
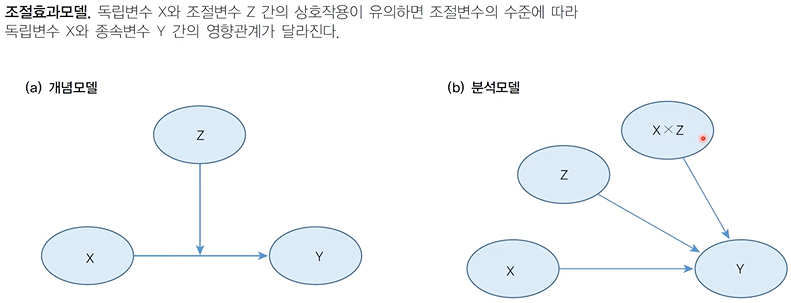
-> 분석모델: X, Z , X x Z (내가 직접 만드는 변수- 상호작용항)

-> 마력이 증가하면 연비가 감소함
-> 무게의 수준에 따라서(z- 조절변수) 연비가 감소하는 정도(독립변수의 영향)가 달라질 수 있는지 검정하고자 함
-> 독립변수: 마력, 무게, 마력 X 무게 (상호작용)
- 마력 X 무게 (상호작용) 이 유의하지 않다면, z (조절변수)의 값이 변화하더라도 x 와 y 의 영향관계는 달라지지 않는다
- 마력 X 무게 (상호작용) 이 유의하다면, z (조절변수)의 값이 변화할 때 x 와 y 의 영향관계는 달라짐
str(mtcars)
model.lm <- lm(mpg ~ hp + wt + hp:wt, data=mtcars)
summary(model.lm)


=> 무게에 따라서 마력이 연비에 미치는 영향이 다름
round(mean(mtcars$wt), 1)
round(sd(mtcars$wt), 1)
library(effects)
windows(width=7.0, height=5.5)
m <- round(mean(mtcars$wt), 1)
s <- round(sd(mtcars$wt), 1)
plot(effect(term="hp:wt", mod=model.lm, xlevels=list(wt=c(m-s, m, m+s))),
lines=list(multiline=TRUE, lwd=2, lty=c(3, 2, 1),
col=c("royalblue", "violet", "maroon")),
main="Interaction Plot for Horsepower and Weight")
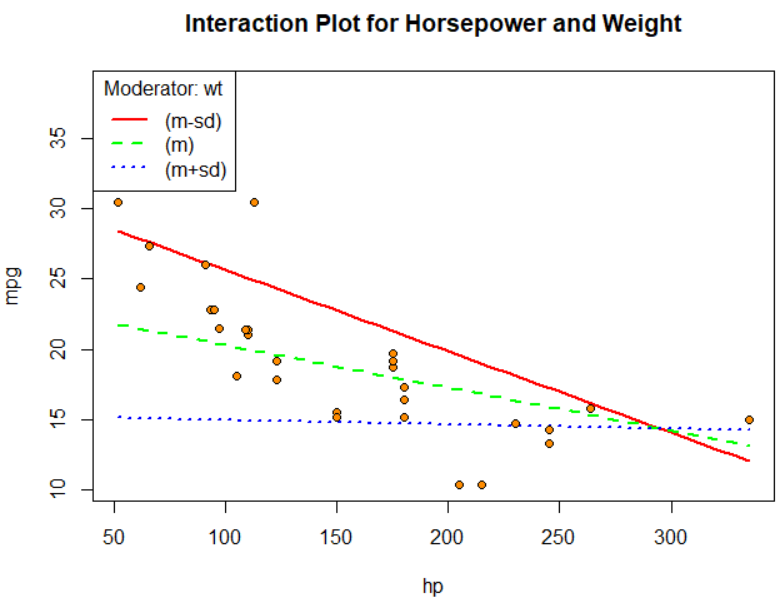
- 평균 무게
- 무게가 작을 때, 연비가 그냥 감소함 (민감하게 반응)
- 무게가 증가할 땐, 연비가 수평 (무게가 중요함: 마력을 증가시켜도 연비가 잘 감소하지 않음)
- 무게가 증가할수록, 회귀계수의 절댓값 크기는 계속 줄어듦
# [그림 7-20]
library(rockchalk)
windows(width=7.0, height=5.5)
plotSlopes(model=model.lm, plotx="hp", modx="wt", modxVals="std.dev.",
pch=21, col=rainbow(3), cex=1, bg="darkorange",
main="Interaction Plot for Horsepower and Weight")
조절매개효과분석
- 매개변수에 의해 매개된 두 변수(독립변수와 종속변수) 간 직접적 또는 간접적 영향 관계에 제 4의 변수 (조절변수)가 영향을 미치는지 검정
- 조절효과는 매개효과모델의 모든 경로에서 발생할 수 있음
1) 매개효과 -> 간접효과
2) 조절매개효과 존재

- 매개변수: 기술습득/ 조절변수: 자기효능감
- 조절효과: 자기효능감 수준에 따라서 간접효과의 영향에 차이가 있는지

- 조절변수: Z
종속변수 M 일 때)
- 독립변수: X, Z, Xx Z
종속변수 Y 일 때)
- 독립변수: X, Z, Xx Z
- 독립변수: M, Z, Mx Z

- 조절변수: am (변속기)
model.M <- lm(wt ~ disp*am, data=mtcars)
model.M <- lm(wt ~ disp + am + disp:am, data=mtcars)
model.Y <- lm(mpg ~ disp*am + wt*am, data=mtcars)
model.Y <- lm(mpg ~ disp + am + wt + am + wt:am, data=mtcars)
- 자동변속기 (am= 0)
-> 간접효과가 작고 (수동변속기에 비해), p-값이 유의수준에 비해 큼 (유의하지 않음)
library(mediation)
set.seed(12)
model.med1 <- mediate(model.m=model.M, model.y=model.Y, covariates=list(am=0),
treat="disp", mediator="wt", boot=TRUE, sims=500)
summary(model.med1)
- 수동변속기 (am= 1)
-> 간접효과가 크고 (자동변속기에 비해), p-값이 유의수준에 비해 작음 (유의함)
set.seed(12)
model.med2 <- mediate(model.m=model.M, model.y=model.Y, covariates=list(am=1),
treat="disp", mediator="wt", boot=TRUE, sims=500)
summary(model.med2)
-
- 차이가 통계적으로 유의한지 검정해야 함
set.seed(12)
model.med <- mediate(model.m=model.M, model.y=model.Y,
treat="disp", mediator="wt", boot= TRUE, sims=500)
set.seed(12)
test.modmed(object=model.med,
covariates.1=list(am=0), covariates.2=list(am=1), sims=500)
-
-
'통계' 카테고리의 다른 글
| [통계 데이터분석] 패널티회귀분석 (0) | 2024.12.01 |
|---|---|
| [통계데이터분석] 패널티회귀분석 (0) | 2024.11.25 |
| [통계데이터분석] 다항회귀분석, 다중회귀분석 (0) | 2024.11.10 |
| [통계 데이터분석] 회귀분석- 단순회귀분석 (0) | 2024.11.04 |
| [통계 데이터 분석] 독립성검정과 적합성검정 (0) | 2024.11.02 |



