| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 연속확률분포
- 머신러닝
- 방학
- 오블완
- 데이터분석
- 정기시험
- 독학
- 데이터분석프로젝트
- WISET
- 절사평균
- 인스타툰 #지식 #클래스101 #전자책 #인스타그램 #인스타 #만화 #웹툰 #아이패드드로잉
- dsa프로젝트
- 평균
- 기하분포
- 기술통계
- 데이터독학
- 3ㅣ
- 베르누이
- 신청
- r #데이터분석 #adsp #자격증 #대외활동 #여름방학 #취업준비
- 3과목
- ADSP
- 티스토리챌린지
- 옻
- 자격증
- 파이썬
- 이항분포
- R
- 대학생
- 분위수
- Today
- Total
mmings_pring_day
[통계 데이터분석] 회귀분석- 단순회귀분석 본문
회귀분석
- 변수 (독립변수 및 종속변수) 간의 관계를 나타내는 선형회귀을 도출하여 변수 간 연관성을 분석
(어떤 두 변수의 관측값을 이용해서 둘 간의 관게를 그래프로 표현하면, 두 변수 간의 대략적인 관계 패턴을 파악할 수 있음)
-> 산점도로부터 이 두 변수 간에 존재하는 일정한 모양의 패턴을 관찰할 수 있음
-> 이 패턴을 수리적인 모델로 표현할 수 있다면, 변수 간의 관계를 설명하는 적절한 도구로 활용할 수가 있고, 이를 이용해서 한 변수의 값을 알고 있을 때 다른 변수의 값을 예측하는 것도 가능함
(예: 광고비와 매출액의 관측값을 산점도 상에 표현하였더니, 하나의 직선을 따라서 주변에 분포하는 패턴을 보인다면, 그 직선을 표현하는 하나의 방정식을 도출해서 두 변수 간의 관계를 설명하는데 활용할 수 있음)
-> 이 직선을 나타내는 방정식을 '선형회귀 모델' 또는 '선형 회귀식'이라고 얘기함
-> '선형 회귀식'을 도출해서 변수 간의 연관성을 분석하는 통계 기법을 '회귀 분석'이라고 얘기 함
- 단순회귀분석
: 한 개의 연속형 독립변수를 이용하여 한 개의 연속형 종속변수를 예측
- 다항회귀분석

: 한 개의 연속형 독립변수를 이용하여 한 개의 연속형 종속변수를 예측
: 한 개의 독립변수를 n 차 다항식의 형태로 선형결합해서 모델링을 한 형태의 회귀식
[단순회귀분석 과 다항회귀분석 의 차이]
- 'x' 라는 독립변수가 하나 있을 때, 'x'라는 독립변수를 그대로 사용하게 되면 '단순회귀 분석' 이 됨
- 그 'x' 라는 독립변수를 x 제곱 항을 만들고, x 세제곱 항을 만들어서 동일한 x 란 독립변수로부터 x 항과 x 제곱 항과 x 세제곱 항, 세 개를 만들어서 이 세 개를 독립변수로 활용할 경우에, 우리는 다항회귀 분석을 수행할 수가 있음
(실질적으로, x 항과 x 제곱항과 x 세제곱 항이 있기 떄문에 마치 두 개 이상의 독립변수가 있는 것처럼 보여서 형태 상으로 다중회귀분석과 유사함 -> 다항회귀분석은 다중회귀분석의 특수한 한 형태라고 볼 수가 있음.)
- 다중회귀분석
: 두 개 이상의 연속형 독립변수를 이용하여 한 개의 연속형 종속변수를 예측
*회귀분석을 위해서, 일반적으로 변수들은 모두 간격 척도나 비율 척도로 측정된 이런 연속형 변수여야 함*
[ 많은 직선 중에서 종속변수를 맞추는 독립변수를 구하기 (모든 관측값에 대해서 직선 과의 거리 재기) ]
1) 상관분석을 통해 도출한 상관계수는 가상의 직선 상의 데이터 점들이 얼마나 가까이 모여 있는지를 알려주지만, 그 직선이 어떻게 생겼는지는 구체적으로 알 수가 없음
-> 한 변수 값으로부터 다른 변수값을 예측하고자 한다면, 그 직선에 대한 좀 더 많은 정보가 필요함
(예: 직선의 기울기와 절편 같은 정보가 필요함)
- 회귀 분석을 통해서 이러한 직선의 방정식을 구할 수가 있음. 여기에서는 우선 하나의 독립변수를 갖는 단순회귀분석을 통해서 회귀식을 도출하는 과정을 살펴보겠음
(예: 한 국가의 기대수명에 영향을 미치는 요인으로, 그 국가의 도시인구 비율을 선정하고 그들 간의 관련성을 '선형회귀식' 모델을 이용해서 분석한다고 가정해 보겠음
-> 기대수명은 종속 변수로서 역할을 하게 되고, 도시 인구 비율은 종속변수를 설명하는 독립변수로서 역할을 수행하게 됨

[그래프 해석]
- 도시인구비율과 기대수명 간의 관측값들을 산점도상에 표현하면 산점도 상의 점들은 일정한 패턴을 갖고 있음.
=> 도시 인구 비율이 높은 국가는 그렇지 않은 국가에 비해서 대체적으로 기대수명이 더 김
=> 도시인구 비율의 증가에 따라서 기대수명은 증가하는 경향을 보임
-> 각 변수값을 나타내는 점들은 하나의 가상의 직선을 따라 주변에 분포하고 있음
=> 따라서, 두 변수는 선형관계를 가지고 있다고 말할 수 있음
=> 도시 인구비율이 증가함에 따라 기대수명 역시 증가하는 모양을 보이기 때문에 두 변수는 '정의 선형관계'를 가짐
but, 모든 관측값들이 직선과 정확히 일치하지는 않음
-> '직선과의 정확한 일치'는 불가능한 것은 아니지만, 발생할 가능성은 상당히 희박함
(if 모든 점이 직선상에 정확히 놓여질 수 있다면, 우리는 그 직선을 이용해서 두 변수 간의 관계를 완벽하게 설명할 수 있음
-> 그림: 관측값들은 가상의 직선은 주변에 분포되어 있는 것으로 가정할 수 있을 뿐이지, 정확히 직선상에 높여 있지는 않음.
-> 산점도: 관측값들 사이를 통과해서 그려줄 수 있는 직선은 하나만 있는 것이 아니고, 여러 개의 직선이 존재할 수 있음
=> 따라서, 두 변수 간의 관계를 적절히 설명/ 예측하기 위해선, 관측값들 간의 관계를 가장 잘 설명해줄 수 있는 '단 하나의 직선'을 구하는 체계적인 방법이 요구가 됨
- 최소자승법: 그러한 직선을 구하는 방법으로써, 가장 많이 사용되는 회귀식 도출 방법
-> 최소자승법: 산점도 상에 관측된 각 좌표점과 임의의 작선 사이의 수직거리를 제곱해서 합한 값이 가장 작게 되는 직선을 찾는 방법
(최소자승법에 의해서 구해진 직선을 최소자승회귀선 또는 회귀선이라고 함. )

1) 그래프에서 볼 수 있듯이, 각 관측값과 회귀선 간의 수직선을 그림
2) 그 거리를 측정헤서 '관측점과 회귀선 간의 거리를 계산'함.
3) 그런 다음에, 각 관측점과 회귀선 간의 거리를 각각 제곱하고 모두 더해서 '거리 제곱의 합'을 구함
=> '최소자승회귀선'은 이렇게 구해진 거리 제곱의 합이 그밖에 다른 어떤 직선에 대해서 구해진 거리 제곱의 합보다 작게 되는 직선을 말함
=> '최소자승회귀선'은 이와 같은 직선의 방정식으로 나타낼 수가 있음
*y: 수직 축 상의 변수를 나타내며, 종속 변수/ x: 수평 축 상의 변수를 의미하고, 독립 변수
Bo: 절편으로, x 값이 0일 때의 y 값을 의미함/ B1: 기울기 (x 한 단위 변화량에 대한 y 의 변화량을 나타냄) *
(종속 변수: 기대수명, 독립변수: 도시인구 비율
=> 종속변수는 독립변수에서 예측되기 때문에 독립변수인 '도시인구 비율'을 이용해서 종속변수인 '기대수명'을 예측할 수 있음.


=> 기대수명 과 도시인구비율 을 이용해서 이와 같은 '회귀식'을 도출할 수 있음
: 회귀식을 그래프로 표현하면, 왼쪽 직선 그래프 형태로 표현될 수 있음
(기울기: 0.48 -> 도시인구 비율 한 단위의 증가 (= 1% 증가)는 기대수명 0.48 의 증가를 가져오는 것을 이해할 수 있음)
-> 회귀식을 이용하면 도시인구비율이 50% 인 나라는 50% * 0.48 + 41.0 으로 계산해서 기대수명이 65세라고 예측할 수 있음 [기대수명= 41.0 + 0.48 *도시인구비율]
-> 도시인구비율이 51% 인 경우 = 41.0+ 0.48 * 51 = 65.48 세가 예상 기대 수명이 됨
-> 이 65세와 '65.48세'의 차이 = 0.48 로써 회계식의 기울기와 일치함
(x 축의 독립 변수의 값이 1만큼 증가할 때 y 축의 종속 변수의 값이 변화하는 양이, 회귀식의 기울기이기 때문에 종속 변수 값의 차이는 결국 회귀식에서 기울기에 해당이 됨

- 기울기 > 0 : 독립변수의 증가는 종속변수의 증가를 가져옴
- 기울기 < 0 : 독립변수의 증가는 종속변수의 감소를 가져옴
(=> 양수든, 음수든 절댓값 준으로 '기울기의 값이 크면 그 변화의 폭은 커지고, 반대로 기울기의 값이 작으면 그 변화의 폭은 작아짐)
- 기울기 = 0 : 모든 독립변수에 대해서 종속변수 값이 일정함
(독립변수가 종속변수에 아무런 영향을 미치지 않았음을 의미하고, 이런 두 변수 간의 어떠한 선형 관계도 존재하지 않음을 뜻함 => 위의 그래프처럼 수평선으로 그려지게 됨)
- if 독립변수와 종속변수가 서로의 역할을 바꾸게 되면) 기울기와 절편은 값이 달라짐
=> 서로 대칭인 특성을 갖는 상관 계수와 달린, 회귀선의 기울기와 절편은 비대칭적인 특성을 갖음
=> 따라서, 어떤 변수가 독립변수이고, 어떤 변수가 종속변수인지 회귀식의 도출에 있어서 중요한 고려사항이 될 수가 있음
* 절편에 어떤 의미를 부여할 때) 주의를 기울일 필요가 있음*
절편: 독립변수의 값이 0일 때, 종속변수의 값을 의미하기 때문에 -> '독립변수의 값이 0' 이라는 것이 의미있는 숫자가 아닌 한, 절편이 갖는 의미는 제한적일 수밖에 없음
(에: 기대수명을 산출할 수 있는 국가 중에서도 도시인구비율이 0인 나라는 실제로 존재할 가능성이 매우 작기 때문에, 도시인구비율이 0인 가상의 국가에 대한 기대수명에 실질적인 의미를 부여하기는 힘듦.
=> 기대수명과 도시인구비율 간에 이러한 회귀식이 도출됐다고 해서, 도시인구비율이 0일 때 그 국가의 기대수명이 41세다 말할 땐 우리가 주의를 기울일 필요가 있음
- car 패키지에 포함되어 있는 prestige 데이터셋 이용 : 회귀분석 수행
- Prestige 데이터셋: 직업별로 평균 교육시간, 평균 소득, 여성 비율, 직업 명망도, 직업 유형 등의 데이터가 기록되어 있음
- 교육기간 (education)과 소득(income) 간의 관계 분석
- 교육기간은 '연 단위', 소득은 '달러 단위'
- lm( ) 함수 이용: 회귀분석 수행
library(car)
str(Prestige)
- Prestige.lm 이란 변수에 '회귀분석 수행 결과' 저장
#lm()함수의 첫번째 인수(formula): 종속(income) ~ 독립(education)
#lm()함수의 두번째 인수: 사용할 데이터셋 지정
Prestige.lm <- lm(income ~ education, data=Prestige)
class(Prestige.lm)
Prestige.lm
[결과]: 회귀식의 절편과 기울기를 확인가능- 절편: (intercept) -2853.6- 기울기: 898.8-> 이 회귀식을 산점도 상의 직선으로 그려볼 수 있음
- plot( ) 함수: 산점도 생성 함수 (시각화)
windows(width=7.0, height=5.5)
# plot()함수의 첫번쨰 인수(formula): 종속(소득) ~ 독립(교육기관)
plot(Prestige$income ~ Prestige$education,
pch=21, col="blue", bg="cornflowerblue",
xlab="Education (years)", ylab="Income (dollars)",
main="Education and Income")
[결과]: 교육기관이 증가할수록 소득이 증가하는 패턴을 보임 (관계가 명확하진 않음)
-> 이러한 관측값들을 통과하는 회귀식을 만들어서 그래프상에 그려 보겠음
- abline( ) 함수 이용: 회귀식을 산점도상에 그리기 위해서 사용
# abline()함수의 첫번째 인수: 회귀분석 결과 생성된 모델 객체 지정
abline(Prestige.lm, col="salmon", lwd=2)
- 그래프: 교육기관과 소득은 '정의 선형관계'를 갖음
(독립변수에 대한 회귀계수: 898.8 -> 교육기관이 1년 증가할 때마다 소득은 898.8 달러씩 증가함)
- 절편: 독립변수의 값이 0일 때의 '종속변수의 값'을 나타냄 (독립변수의 값이 0 이라는 것이 의미있는 숫자가 아닌 한, 절편이 갖는 의미는 제한적일 수밖에 없음_
(예: 조사된 직업 가운데 '교육기간이 0'인 경우는 실제로 존재하지 않기 때문에 '교육기간이 0'인 가상의 직업에 대한 소득의 실질적 의미를 부여해서는 안 됨/ 여기 절편의 값이 '-2853.6' 이라 해서, 교육기간이 0일 때 소득은 '-2853.6' 이다라고 얘기하는 것은 문제가 있을 수 있음)
[R 의 회귀모델 분석 결과 추출 함수]
- 용도별 추출 함수 이용: 선형회귀식의 회귀계수 정보 이욍 좀 더 다양한 통계 분석 결과를 보기 위함
-> 회귀 모델 객체에 포함된 분석 결과를 추출할 때, 이런 함수를 이용 가눙!
-> 회귀 모델 객체로부터 분석 결과를 추출하는데 이용할 수 있는 주요 함수
- anova( ) 함수: 분산 분석표 추출 함수
- coefficient( ) 함수: 회귀계수 추출
- coef( ) 함수: 회귀계수에 대한 신뢰구간을 추출
- fitted( ) 함수: 회귀식에 의한 예측값 산출
- residuals( )함수/ resid( ) 함수: 잔차(관측값과 예측값 간의 차이) 산출
- summary( ) 함수: 주요 분석 정보(잔차, 회귀계수, R^2, F값) 요약 산출

- summary( ) 함수 이용: 회귀 분석 결과를 주요한 정보 위주로 추출
# summary() 함수의 인수: 회귀모델 객체를 인수로 지정
summary(Prestige.lm)
[결과] summary( ) 함수를 통해서 여러 가지 많은 정보를 확인 가능
1) Residuals (잔차의 분포) => 잔차: 관측값- 예측값
-> 잔차가 작을수록 좋은 모델임! (관측값과 예측값 간의 거리가 작다는 것임)
-> 이상적인 회귀 모델은 정규분포를 형태를 따름 (평균이 0인)
-> 잔차의 평균이 '0' 이기 때문에 중위수의 부호를 통해서 분포의 치우침 정도를 학인 가능
* median 값(중위수): -41.9 => '평균이 0' 보다 왼쪽에 있으므로 잔차는 종 모양의 전형적인 정규분포에 비해 약간 오른쪽으로 꼬리가 긴 모형 (perfect 하지 않은 모델임) *
2) Coefficients (회귀계수 추정치 및 유의성 검정)
-> 회귀계수의 추정치 (estimate), 표준오차 (Std. error), t 값(t value), p-값 확인 가능
-> 회귀계수에 대한 t 검정은 회귀계수가 0 이라는 귀무가설을 검정
-> '독립변수 education 에 대한 p- 값'은 유의수준 0.05에 비해 매우 작으므로 회귀계수의 추정치는 통계적으로 유의함
(즉, '독립변수 education 의 회귀계수 = 0'이라고 할 수 없음)
3) Residual standard error (잔차의 표준오차 = 잔차가 변동하는 정도)
: 회귀모델을 이용하여 독립변수로부터 종속변수를 예측할 때 발생하는 잔차의 표준편차를 의미함
=> 즉, RSE 는 회귀선을 중심으로 상하로 변동하는 관측값의 평균 변동성을 나타냄. RSE 는 모델에 의해 설명되지 않는 데이터의 패턴을 보여주는 척도이므로 작은 RSE 는 모델의 적합도가 좋다는 것을 의미함 => 작을수록 좋음
4) R&^2 (Multiple R-squared) : R^2 = 회귀모델의 설명력을 나타냄
: R^2 0.3336 -> 회귀모델이 종속변수인 소득 변동성(분산)의 33.36% 를 설명한다는 것을 나타냄
=> R^2 값은 그 값이 클수록 회귀 모델의 설명력이 좋다는 것을 의미함
5) F-statistic (회귀식의 유의성 검정)
: F 값을 통해 회귀모델의 유의성 검정 결과를 확인할 수 있음.
-> '회귀계수가 모두 '0' 이라는 귀무가설'을 검정함
-> 회귀계수 가운데 어느 하나라도 0 이 아니면 회귀모델은 통계적으로 유의함
* 단순회귀분석 이기 때문에 -> 회귀 모델에 포함된 회귀계수가 한 개 밖에 없기 때문에, 결국 회귀식의 유의성 검정과 회귀계수의 유의성 검정이 같은 것을 의미한다는 것을 얘기할 수 있음
=> p-값 은 유의수준 0.05 에 비해 매우 작으므로 회귀모델은 통계적으로 유의하다라는 것을 의미함
= 회귀식에 포함되어 잇는 회귀게수 가운데 어느 하나라도 0이 아니라는 얘기임 (단순회귀분석은 '회귀계수'가 하나밖에 없기 때문에 모든 회귀계수가 0이 아니라는 것을 얘기함
[회귀식의 유의성 검정 과 회귀계수의 유의성 검정 간의 관계]
-> 단순회귀분석의 경우) 회귀계수가 하나밖에 없기 때문에 회귀식의 유의성 검정은 회귀계수의 유의성 검정과 동일함
-> but, 독립변수가 두 개 이상인 다중회귀분석의 경우) 두 검정은 서로 다른 의미를 가짐
= 회귀식의 유의성 검정은 모든 회귀계수가 0인지 검정하며, 회귀계수의 유의성 검정은 특정 회귀계수가 0인지 검정
[회귀계수 값과 그에 대한 유의성 검정 결과]
- summary 함수로부터 출력된 결과에 coef( ) 함수를 적용하면 -> 회귀계수에 대한 추정치, 표준오차, t값, p- 값 등을 테이블 형태로 추출 가능
- summary( ) 함수로부터 전반적인 회귀분석 결과를 확인할 수 있지만, 용도별 추출 함수 이용) 필요한 정보만을 추출하거나 좀 더 자세한 정보를 얻을 수 있음
Prestige.lm.summary <- summary(Prestige.lm)
coef(Prestige.lm.summary)
anova(Prestige.lm)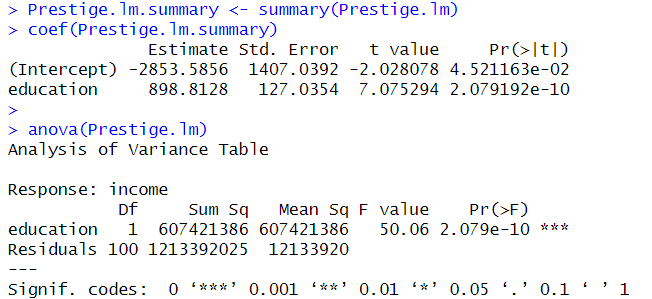
- 회귀모델 객체에 anova( ) 함수 적용: 회귀모델에 대한 분산분석표를 얻기 위함일 때
- '회귀모델에 대한 분산분석표': 회귀식의 유의성 검정에 활용됨
-> p-값이 유의수준 0.05 에 비해 매우 작으므로 회귀계수가 모두 0 이라는 귀무가설을 기각할 수 있고, 따라서 회귀식은 통계적으로 유의함
- anova( ) 함수: 데이터프레임 형식으로 결과 반환 (분산분석표로부터 특정 원소만을 추출 가능)
rownames(anova(Prestige.lm)); colnames(anova(Prestige.lm))
anova(Prestige.lm)["education", "Pr(>F)"]
anova(Prestige.lm)[1, 5]
- coef( ) 함수 이용: 회귀모델 객체로부터 회귀계수만을 추출할 수 있는 함수
- -> 절편과 기울기만이 추출됨
coef(Prestige.lm)
- confint( ) 함수 이용: 회귀계수에 대한 신뢰구간 계사한하는 함수
- -> 달리 지정하지 않으면, 기본값으로 95% 신뢰구간이 산출됨
- level 인수를 이용 -> 신뢰구간의 신뢰수준을 지정할 수 있음
confint(Prestige.lm)
confint(Prestige.lm, level=0.99)
- fitted( ) 함수: 회귀식에 의한 예측값을 벡터 형태로 반환
- -> fitted(Prestige.lm)[1:3] ; fitted( ) 함수 내에, 회귀모델 객체를 지정하고 그 결과를 앞의 세 개만을 출력해 보겠음
- -> 앞의 세 개의 직업에 대한 회귀식에 의한 예측값을 산출 가능
- resid( ) 함수: 관측값과 예측값 간의 잔차 산출하는 함수
- 예: 데이터셋에 포함된 처음 세 개 직업에 대해 회귀식에 의한 소득의 관측값과 에측값 간의 잔차 구하기
- Prestige$income[1:3]: 앞의 세 개의 '실제 값'
- Prestige$income[1:3] - fitted(Prestige.lm[1:3]) = resid(Prestige.lm)[1:3]
#Prestige$income[1:3] - fitted(Prestige.lm[1:3]) = resid(Prestige.lm)[1:3]
fitted(Prestige.lm)[1:3]
resid(Prestige.lm)[1:3]
Prestige$income[1:3]
[회귀모델: 기본적으로 두 변수 간의 관계를 설명하는 역할을 하지만, 새로운 데이터에 대한 예측값을 추정하는 데도 유용하게 활용 가능]
- predict( ) 함수: 교육기간이 각각 5년, 10년, 15년일 때의 소둑을 예측하는 함수
- -> 이러한 예측 작업을 위해서는, 예측에 사용할 데이터를 '데이터프레임' 형식으로 생성해야 하고, 그 '데이터프레임'에 예측 변수 이름을 독립변수 이름과 같은 이름으로 지정해 줘야 함
- -> 데이터셋을 생성
- predict( ) 함수: 새로운 데이터프레임을 생성하고 데이터프레임에 포함되어 있는 값들에 대한 예측값을 만들기 위해서 사용
Prestige.new <- data.frame(education=c(5, 10, 15))
# predict()함수의 첫번째 인수: lm()함수로부터 나온 모델- 회귀모델 지정
# predict()함수의 두번째 인수(newdata): 예측 변수가 포함되어 있는 새로운 데이터셋 지정
predict(Prestige.lm, newdata=Prestige.new)
- 실행결과) 교육기관이 5년일 때, 10년일 때, 15년일 때 소득 확인 가능
- interval= "confidence" ) 각 예측값에 대한 95% 신뢰구간을 구할 수 있음 -> 종속변수의 모집단평균에 대한 95% 신뢰구간
predict(Prestige.lm, newdata=Prestige.new, interval="confidence")

[95% 신뢰구간에 따르면]
: 교육기간이 10년인 직업의 실제 평균 소득이 5,425 달러에서 6,844 달러 사이에 존재할 가능성이 95%
: 즉, 교육기간이 10년인 직업에 대한 소득의 모집단평균이 이 두 구간 사이에 있을 가능성이 95%
- subset 인수 ) 데이터셋 전체가 아닌 일부 서브셋에 대해서만 회귀분석 수행 (서브셋 조건 지정)
- 예: 평균보다 더 많은 교육을 받은 집단과 그렇지 않은 두 집단에 대해 각각 회귀분석 수행 가능
mean(Prestige$education)
lm(income ~ education, data=Prestige, subset=(education > mean(education)))
lm(income ~ education, data=Prestige, subset=(education <= mean(education)))[분석결과]
- 평균 교육기간: 10.73
(현재 데이터셋에 포함되어있는 직업들에 대한 평균 교육 기간)
-> '이 기간보가 긴 집단에 대한 회귀 분석 결과'와 '이 기간보다 더 작은 집단에 대한 회귀분석 결과' 각각 수행해 보기

[분석결과]
- 서브셋 조건 지정 : education > mean(education)
: 교육기간이 평균보다 큰 집단에 대해서만 회귀분석을 수행함
= 교육기간이 평균보다 큰 경우: 교육기간이 1년 늘어나면 소득은 1,455 달러 증가
= 교육기간이 평균보다 작은 경우: 교육기간 1년 당 281.8 달러의 소득 증가에 그침
=> 두 집단에 있어서 회귀선의 기울기가 다르다는 것! : 단일직선의 회구선보다는 한 개의 굴절을 갖는 곡선에 의해 교육기간과 소득 간의 관계를 좀 더 잘 설명할 수 있을지도 모른다는 것을 나타냄
-
-
자료출처: https://www.youtube.com/watch?v=8opxpVeWmGY&list=PLY0OaF78qqGAxKX91WuRigHpwBU0C2SB_&index=24
https://github.com/kykwahk/Statistics-R/blob/master/Statistics-R_07.R
Statistics-R/Statistics-R_07.R at master · kykwahk/Statistics-R
『R을 이용한 통계데이터분석(제2판)』(곽기영, 도서출판 청람). Contribute to kykwahk/Statistics-R development by creating an account on GitHub.
github.com
'통계' 카테고리의 다른 글
| [통계 데이터분석] 더미변수 회귀분석/ 매개효과/ 조절효과 (0) | 2024.11.18 |
|---|---|
| [통계데이터분석] 다항회귀분석, 다중회귀분석 (0) | 2024.11.10 |
| [통계 데이터 분석] 독립성검정과 적합성검정 (0) | 2024.11.02 |
| [통계 데이터 분석] 상관분석-자체 (0) | 2024.10.28 |
| [통계 데이터분석] 상관분석 - 상관관계 (0) | 2024.10.27 |



