| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 데이터분석프로젝트
- 이항분포
- 데이터독학
- 데이터분석
- 머신러닝
- 오블완
- r #데이터분석 #adsp #자격증 #대외활동 #여름방학 #취업준비
- 독학
- WISET
- ADSP
- 기하분포
- 옻
- 평균
- 분위수
- 3ㅣ
- 대학생
- 기술통계
- 정기시험
- 인스타툰 #지식 #클래스101 #전자책 #인스타그램 #인스타 #만화 #웹툰 #아이패드드로잉
- R
- 자격증
- dsa프로젝트
- 방학
- 절사평균
- 티스토리챌린지
- 3과목
- 연속확률분포
- 신청
- 베르누이
- 파이썬
- Today
- Total
mmings_pring_day
[통계 데이터분석] 상관분석 - 상관관계 본문
0. 상관관계
- 두 사건 간의 '연관성' 분석
(예: 기업의 연구개발 투자와 신제품 출시 비율 간의 관계, 광고비와 매출액 간의 관계, 한 나라의 일인당 GDP 와 국민의 기대수명 간의 관계 등)
- 두 사건, 즉 두 변수 간의 선형적 관계를 '상관'이라고 하며, 이러한 관계에 대한 분석을 [상관분석]
선형적 관계: 직선으로 올라가는 관계 / 비선형적 관계: 곡선으로 올라감
- 이때 그 두 사건의 대응되는 두 변수는 일반적으로 '연속형 변수'를 가정함
- MASS 패키지의 cats 데이터셋 이용
- cats 데이터셋 = 고양이의 성별(sex)에 따른 몸무게(Bwt)와 심장무게(Hwt)가 기록되어 있음
- 몸무게는 킬로그램(kg) 단위, 심장무게는 그램(g) 단위 : 연속형 변수
# 1. 상관분석 수행 전, 먼저 고양이의 몸무게와 심장무게 간의 대략적인 관계를 산점도를 통해서 살펴보기
-> 산점도 (두 변수 간에는 정(+)의 선형관계가 존재함)
-> 몸무게가 증가할수록 이에 비례하여 심장무게 또한 증가하는 경향
library(MASS)
str(cats)c
- plot() 함수: 두 변수 간의 선형적 관계 '산점도'로 그리는 함수
# plot()의 첫번째 인수(formula): 종속(y축) ~ 독립(x축)
plot(cats$Hwt ~ cats$Bwt,
pch=21, col='forestgreen', bg='green3', las=1,
xlab= 'Body weight(kg)', ylab= 'Heart weight(g)',
main= 'Body weight and Heart weight of Cats')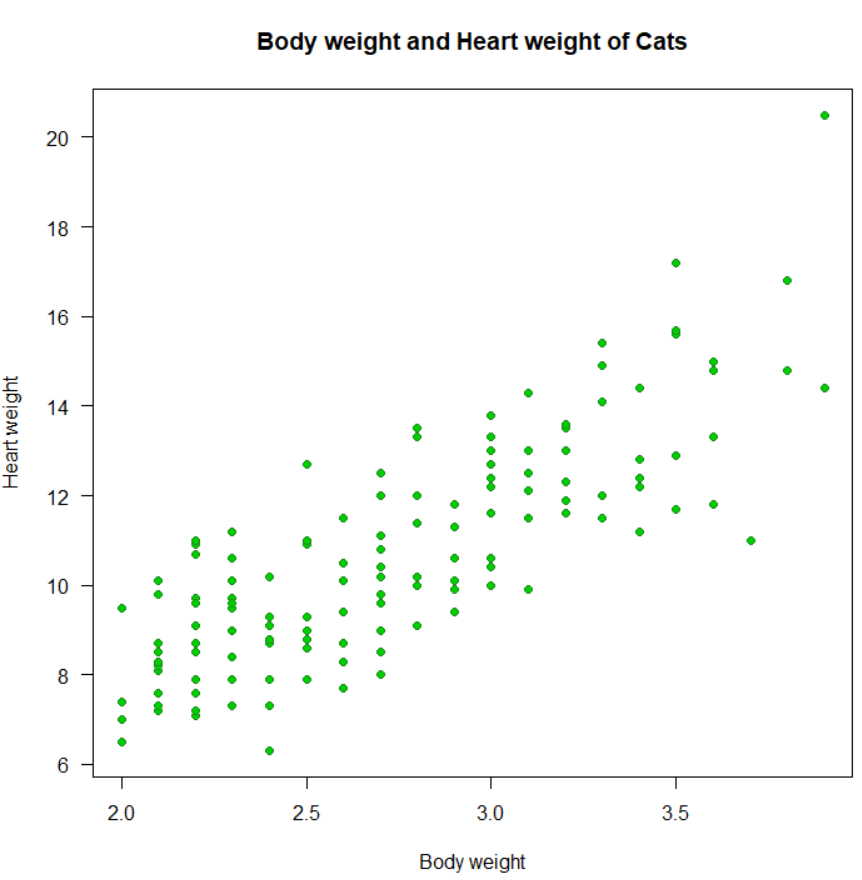
- x축: 고양이의 몸무게, y축: 고양이의 심장 무게 (고양이의 몸무게가 증가할수록 심장 무게 역시 증가하는 패턴을 보임)
-> 산점도를 이용하면 '변수 간의 관계 패턴'을 이해할 수 있음. 하지만 선형관계의 강도를 객관적으로 파악할 수는 없음.
(고양이의 몸무게와 고양이의 심장 무게 간에는 선형적으로 비례하는 관계가 있는 것처럼 보이지만, 그 관계의 강도가 어느 정도인지 수치로 객관하해서 표현할 수는 없음)
- 상관계수= 두 변수 간의 선형 관계의 강도를 측정한 지표
-> 두 변수 간의 선형관계의 강도는 '상관계수'로 측정
(-1 ~ +1 사이의 값을 가짐. 0 일 경우엔 두 변수 간의 선형관계가 없음을 뜻함)
('-' 의 상관계수 = 부의 선형관계 ('-1' 은 완전한 부의 선형관계)/ '+'의 상관계수 = 정의 선형관계를 나타냄 ('+1' 은 완전한 정의 선형관계) )
if 두 변수 간의 상관계수 = '-1' or '+1' -> 하나의 변수로부터 나머지 하나의 변수를 완벽하게 예측할 수 있다는 것을 의미함
(직선 상에 모든 점들이 위치함!)
* 포물선 그래프: 관계는 있으나 '선형관계'는 아님! (관심 대상이 아님!)

- 상관계수의 특징
1) 상관계수는 서로 대칭 임
-> 두 변수 x 와 y 의 상관계수는 y 와 x 의 상관계수와 일치함. 또한 상관계수는 선형변환에 의해 영향을 받지 않음. 변수값에 일정 상수를 더하거나, 빼거나, 곱하거나, 나누어도 상관계수는 변하지 않음.
-> 이는 관측값이 어떤 단위로 측정되었든 간에 변수 사이의 상관계수는 항상 일정하다는 것을 의미함.
(예- 키와 몸무게 간의 상관계수를 구할 때, 인치와 파운드 로 측정된 키와 몸무게 간의상관계수나 센티미터와 킬로그램으로 측정된 두 변수 간의 상관계수는 서로 일치함)
예를 들어, 키와 몸무게의 상관계수를 구한다고 합시다.
사람의 키는 인치(inch) 단위로, 몸무게는 파운드(pound) 단위로 측정할 수도 있고, 키는 센티미터(cm) 단위로, 몸무게는 킬로그램(kg) 단위로 측정할 수도 있습니다.
인치와 파운드 단위에서 상관계수를 계산했다고 가정해 봅시다.
예를 들어, 인치와 파운드로 측정된 값들이 xxx와 yyy라면, 이들 간의 상관계수 Corr(x,y)\text{Corr}(x, y)Corr(x,y)가 있을 것입니다.이제, 같은 데이터를 센티미터와 킬로그램 단위로 변환해 보겠습니다.
키와 몸무게의 측정 단위가 변할 뿐, 키와 몸무게 간의 상관성 자체는 변하지 않습니다.
(인치를 센티미터로 변환할 때에는 인치 값에 약 2.54를 곱하고, 파운드를 킬로그램으로 변환할 때에는 파운드 값에 약 0.4536을 곱하는 것처럼, 각 측정값에 고정된 숫자를 곱하는 선형 변환이 이루어짐.이 선형 변환은 각 변수의 스케일이나 단위를 바꾸지만, 키와 몸무게가 서로 어떻게 변동하는지(즉, 상관성)에는 영향을 주지 않음.
-> 인치와 파운드에서 측정한 상관계수는 센티미터와 킬로그램에서 측정한 상관계수와 동일함.)
[결론]
상관계수는 변수 간의 상대적인 변동을 나타내므로 측정 단위가 바뀌는 선형 변환이 적용되더라도 변하지 않습니다.
- cor( ) 함수 이용 = 변수 간의 상관계수를 구하는 함수
- 고양이의 몸무게와 심장 무게 간의 관계를 보여주는 상관계수 구하기
# cor()함수의 첫번째, 두번째 인수: 상관계수를 계산하고자 하는 두 변수를 차례대로 지정함
cor(cats$Bwt, cats$Hwt)
with(cats, cor(Bwt, Hwt))
-> 상관계수의 값은 '-1 ~ +1' 사이의 값을 가지기 때문에, '0.8' 값은 꽤 높은 수준의 연관성을 보여주는 수치라고 볼 수 있음
=> 고양이의 몸무게와 고양이의 심장 무게 간에는 '꽤 밀접한 관련이 있다' 는 결론을 내림

- cor( ) 함수의 'method' 인수 = 상관계수의 종류 지정 가능
-> 기본값) [method = "pearson"]으로 연속형 변수에 대해서 사용되는 '피어슨 상관계수'를 계산함
-> [method= "spearman" / method= "kendall"] 지정 으로 '서열척도로 측정된 데이터의 등위상관계수'를 계산함
- 연속형 변수: [method= "pearson"]
- 서열척도로 측정된 데이터: [method= "spearman"]
- cor( ) 함수의 'use' 인수 = 상관계수 계산 방법 결정 가능 (데이터셋에 결측값이 포함되어 있는 경우)
-> 기본값) [use= "everything"] 으로 '결측값이 포함되어 있을 경우 NA 가 출력됨'
(결측값이 있는 경우는 사용하지 못함!)
-> [use= "complete.obs"] 은 '하나라도 결측값을 포함하고 있는 케이스는 상관게수 계산 시 제외함'
(드문드문 결측값이 포함되어 있는 경우엔, 포함된 행이 모두 삭제가 되기 때문에 분석에 사용할 수 있는 표본 크기가 줄어드는 단점이 존재함)
(결측값이 있는 경우는 사용하지 못함!)
-> [use= "pairwise.complete.obs"] 은 '분석에 사용되는 변수에 대해서만 결측값이 존재할 때 해당 케이스를 분석에서 제외함'
(상관계수는 '어떤 두 변수간의 관계를 분석하는 것'이기 때문에, 두 변수 내에 결측값이 포함되어 있지 않으면 모든 데이터셋 이용 가능/ 반면에 어떤 두 변수의 상관계수를 계산할 때 결측값이 포함되어 있을 때는 결측값이 있는 행만 삭제해서 계산함)
-> 그래서 'complete.obs' 를 이용하는 경우보다 좀 더 많은 데이터 표본을 이용할 수 있는 장점이 있음
-> 하지만, 상관계수를 계산하는 변수쌍마다 사용되는 케이스 개수가 다를 수 있다는 단점도 있음
0-1. Pearson 상관계수 vs Spearman 상관계수
- 피어슨 상관계수는 '정규성의 가정'을 필요로 함
-> 상관관계를 측정하고자 하는 두 변수는 정규 분포를 따라야 함
if) 정규성의 가정을 충족하지 못할 때 : 데이터값을 순위 (rank)로 대체하여 상관계수를 계산할 수 있음
- 스피어만 상관계수는 정규성 가정을 충족하지 못하는 서열척도의 데이터를 바탕으로 계산됨
-> 순위 데이터를 바탕으로 계산되기 때문에 이상점에 덜 민감
-> 따라서 피어슨 상관계수에 영향을 미칠 것으로 예상되는 이상점이 데이터에 포함되어 있을 때, 스피어만 상관계수가 대안으로 고려될 수 있음
- 피어슨 상관계수와 스피어만 상관계수가 많이 다르다면, 피어슨 상관계수에 큰 영향을 미치는 이상점이 데이터에 포함되어 있을 가능성이 있음
-> 이때, 해당되는 이상점을 찾아 제거한 다음에 '피어슨 상관계수'를 계산하면, '이상점을 제외한 나머지 데이터 간의 연관성'을 피어슨 상관계수로 비교적 잘 나타낼 수 있음
- cor( ): 상관계수 계산 함수이지만, '상관계수'에 대한 유의성 검증을 하진 않음
- cor.test( ): 상관계수에 대한 유의성 검정하 함수
- 귀무가설: 모집단에서 상관계수가 '0' 이다

- 상관관계를 측정하고자 하는 두 변수의 데이터 벡터를 차례대로 인수로 지정
# with()함수의 첫번째 인수 = 사용하고자 하는 데이터셋 지정
# with()함수의 두번째 인수 = cor.test 결과
# cor.test()함수의 인수 = 종속, 독립
with(cats, cor.test(Bwt, Hwt))

- 검정 결과 p-값이 유의수준 0.05에 비해 매우 작으므로 '귀무가설 기각'할 수 있음
-> 고양이의 몸무게와 심장 무게 간에는 상관관계가 존재한다.
- cor.test( ) 함수에 alternative='greater' 나 alternative= 'less' 를 지정하여 단측 검정을 수행할 수 있으며, conf.level 인수에 신뢰구간의 신뢰수준을 지정할 수 있음
-> alternative= 'greater' ) 귀무가설이 모집단에서 '상관게수가 0보다 작다'라는 것을 검증함
(= 대립가설: '상관계수가 0보다 크다')
-> conf.level= 0.99 ) 신뢰구간의 신뢰 수준 지정 가능: 0.99 값은 '99% 상황에서 가설 검증'할 수 있음
# cor.test()함수의 첫,두번째 인수 = 종속, 독립
# cor.test()함수의 세번째 인수 = alternative 지정 (양측검정인지, 단측검정인지)
# cor.test()함수의 네번째 인수(conf.level 인수) = 신뢰구간의 신뢰수준 지정
with(cats, cor.test(Bwt, Hwt, alternative= 'greater', conf.level= 0.99))
-> 검정 결과 =
( 대립가설: 모집단에서의 상관계수가 0보다 크다/ 귀무가설: 0보다 작거나 같다 )
-> 실제로 관측된 상관계수가 0.8 이고, 그에 대응되는 p 값이 유의수준 0.05 보다 작기 때문에, '귀무가설이 사실이다'라는가정 하에서는, '이렇게 큰 양수의 상관계수가 나올 가능성이 거의 0에 가까울 정도로 희박하다는 얘기'임 = 귀무가설 기각 및 대립가설 채택
-> 고양이의 몸무게와 심장 무게 간에는 '0보다 큰 상관계수가 존재한다 라는 결론'을 내릴 수 있음
with(cats, cor.test(~Bwt + Hwt))
(포뮬러 형식을 이용할 경우, 함수 내에 데이터셋 직접 지정 가능)
# cor.test()함수의 첫번째 인수(formula) = ~종속 + 독립
# cor.test()함수의 두번째 인수 = 데이터셋 지정
cor.test(~Bwt + Hwt, data= cats)
-> 포뮬러 형식 사용) 서브셋별로 함수를 적용할 수 있는 장점이 있음.
(예- 암컷 고양이에 대해서만 상관계수의 유의성을 검정하려면 다음과 같이 subset 인수에 추출하고자 하는 서브셋 조건 (Sex =='F') 을 지정함)
# cor.test()함수의 첫번째 인수(formula) = ~종속 + 독립
# cor.test()함수의 두번째 인수 = 데이터셋 지정
# cor.test()함수의 세번째 인수(subset) = 추출하고자 하는 서브셋 조건 지정
cor.test(~Bwt + Hwt, data= cats, subsets= (Sex=='F'))

-> '암컷 고양이'에 대해서도 '고양이의 몸무게와 심장 무게 간에는 유의한 상관관계가 존재한다'라고 결론을 내릴 수 있음
- iris 데이터셋
-> 데이터셋에 '두 개'를 초과하는 숫자 벡터가 포함되어 있으면, cor( ) 함수는 상관계수 행렬을 생성함
-> iris 데이터셋 을 이용해서 '상관계수 행렬' 생성!
str(iris)
# [두 개를 초과하는 변수 간의 상관관계 검정]
# cor() 함수의 인수: 데이터프레임 지정
cor(iris[-5])
-> 숫자 형식이 아닌 다섯 번째 열을 제외한 네 개 변수 간의 상관계수 행렬을 얻을 수 있음
( iris 데이터셋 = 다섯 번째 열이 'iris' 꽃의 종류를 나타내기 때문에 숫자 데이터가 아님!, 숫자 데이터로 구성된 앞의 4개의 변수에 대해서 cor 함수를 적용해서 네 개 변수 간의 상관계수 행렬을 계산)

-> 결과) 네 개의 변수 간의 상관계수 행렬이 산출된 것을 볼 수 있음
- cor( )함수의 수행 결과 : 변수 이름을 행 이름과 열 이름으로 갖는 행렬 형식으로 출력됨
-> 상관계수를 'iris.cor' 변수에 저장!
iris.cor <- cor(iris[-5])
class(iris.cor)
-> 이러한 행렬로부터, 임의의 두 변수 간의 상관계수를 '행렬 인덱싱'을 이용해서 추출할 수 있음
str(iris.cor)
(예- 'Petal.Width'와 'Petal.Length' 간의 상관계수는 '행과 열의 이름'을 직접 지정해서 추출 가능!)
iris.cor['Petal.Width','Petal.Length']
-> 결과: 'Petal.Width' 와 'Petal.Length' 간의 상관계수가, 상관계수 행렬 로부터 직접 추출된 것을 볼 수 있음
- cor( )함수 => ' 두 개를 초과하는(세 개 이상의 변수)변수 간의 상관계수도 계산해서 '상관계수 행렬 형태'를 구해주지만, 이 '변수들 간의 상관계수'가 통계적으로 유의한지는 알려주지 않음'
- cor.test( ) 함수 => 상관계수의 통계적 유의성 검정을 위해 사용했던 함수/ 두 변수 간 상관계수 유의성 검정에만 사용할 수 있는 한계가 있음 (세 걔 이상의 변수 간의 상관계수에 대한 통계적 유의성 검정은 할 수 없음)
- corr.test( ) 함수 => 두 개를 초과하는(세 개 이상의 변수) 변수 간의 상관계수 유의성 검정과 상관계수를 동시 출력을 위한 함수
-> 행렬이나 데이터프레임을 인수로 받아서 상관계수 행렬과 그에 대응되는 유의확률(p-값) 행렬을 반환함
(예- iris 데이터셋의 네 개 변수 간 상관계수와 대응되는 유의확률 (유의성 검정 결과) 를 corr.test( ) 함수를 사용해서 수행)
library(psych)
corr.test(iris[-5])
(1) 상관계수 행렬이 출력됨
(2) 상관계수 행렬에 대응되는 유의확률이 출력됨
-> 'Sepal.Length' 와 'Sepal.Width' 간 상관계수 '- 0.12' 와 그 에 대응되는 유의확률은 '0.15' 로서 유의수준 0.05 에서 통계적으로 유의하지 않음 (귀무가설을 채택, 대립가설 기각)
-> 표본으로부터 계산된 '-0.12' 라는 상관계수는 '유의수준 0.05'에서 통계적으로 유의하지 않다 라는 결론을 내릴 수 있음
-> 모집단에서 'Sepal.Length'와 'Sepal.Width' 간의 관계는 '상관계수가 0' 일 수도 있다.
- 상관계수 95% 신뢰구간을 출력
print(corr.test(iris[-5], short=FALSE))
-> 마지막 구간에 95% 신뢰구간이 출력된 것을 볼 수 있음
(첫번째 행: 'Sepal Lenght' 와 'Sepal Width' 간의 상관계수와 95% 신뢰구간 정보가 출력된 것을 볼 수 있음)
-> 'raw.r' 의 표본으로부터 계산된 상관계수가 출력되어 있음
(95% 신뢰구간의 하한값: raw.lower_ -0.27/ 상한값: raw.upper_-0.04)
-> 95% 신뢰구간 내에 '0'이 포함되어 있음 (동일하다는 뜻!) => 귀무가설을 기각하지 못함 (채택)
- 세 개 이상의 변수 간 상관계수를 보여주는 상관계수 행렬을 그래프로 시각화
- state.x77 데이터셋 이용
- 미국 50개 주에 대한 정보가 저장된 데이터셋
str(state.x77)- cor( ) 함수: 상관계수 계산하는 함수 (8 변수 간의 상관계수 출력)
old.op <- options(digits= 2)
cor(state.x77)
- pairs.panel( ) 함수 = 산점도, 히스토그램, 상관계수를 동시에 보여주는 함수 (산점도 행렬 그리기)
library(psych)
windows(width=5, height=5)
# pairs.panels()함수의 인수= 데이터셋 지정
# pairs.panels()함수의 나머지 인수= 시각화를 위한 조건 지정
pairs.panels(state.x77,pch= 21, bg='red',hist.col='gold',
main='Correlation Plot of US States Data')
-> 대각선 아래 (산점도), 대각선상 (히스토그램), 대각선 위 (변수 쌍 간의 상관계수) 를 나타냄
- 변수 간 상관계수 행렬을 그래프로 시각화해 주는 함수
- corrgram 패키지의 corrgram( ) 함수 = 변수 간 상관관계를 더 풍부하게 시각화 (원도표, 사선, 색상으로 나타남)
library(corrgram)
windows(width=5, height=5)
corrgram(state.x77)
# lower.panel = 색깔과 사선으로 구분되는 상관관계를 볼 수 있음
corrgram(state.x77,order=TRUE, lower.panel=panel.shade,
upper.panel=panel.pie, text.panel= panel.txt,
main= 'Corrgram of US States Data')

-> 파란색과 왼쪽 아래에서 오른쪽 위로 향하는 사선으로 표현된 셀: 정(+)의 상관관계를 나타냄
-> 빨간색과 왼쪽 위에서 오른쪽 아래로 향하는 사선으로 표현된 셀: 부(-)의 상관관계를 나타냄
-> 색상이 짙을수록 큰 상관관계를 의미함(대각선을 중심으로 위쪽과 아래쪽은 현재 동일한 정보를 표현)
(비슷한 것끼리 모여있음!!)
-> 정의 상관관계: 12시부터 시작해서 시계 방향으로 조각의 색상이 채워짐
-> 부의 상관관계: 12시부터 시작해서 시계 반대 방향으로 조각의 색상이 채워짐
-> 'order= TRUE' : 유사한 상관관계 패턴을 가진 변수끼리 모여있음
# lower.panel = 색깔과 사선으로 구분되는 상관관계를 볼 수 있음
corrgram(state.x77,order=False, lower.panel=panel.pie,
upper.panel=panel.conf, text.panel= panel.txt,
main= 'Corrgram of US States Data')-> 대각선을 중심으로 해서 위쪽: 상관계수와 신뢰 구현을 출력
-> 대각선을 중심으로 해서 아래쪽: 원도표 출력 & 원도표의 색상 변경
편상관계수
: 두 변수 간의 순수한 상관관계 (다른 변수의 영향을 배제함)
: 하나 이상의 다른 변수의 영향을 통제한 상태에서 관심의 대상인 두 변수 간의 선형적 관련성을 측정
1) 두 변수 간의 상관이 존재하는 듯이 보이지만, 사실은 상관관계가 없는 가짜 상관을 찾아내는 데 유용하게 활용됨
(= 두 변수 간의 상관이 두 변수가 진짜 상관을 갖는 제 2의 변수와 상관 관계를 갖기 때문에 발생하는 경우라면, 두 변수 간의 가짜 상관이 관찰될 수 있음)
연봉과 혈압의 관계: 정의 상관관계 (비례적), 숨겨진 변수(제 3의 변수): 나이
(예: 연봉과 혈압~ 나이): 연봉과 혈압 간의 순수한 관계를 분석하고자 한다면 나의 영향을 배제해야 함
-> 나이 변수를 통제해야 함
-> 나이의 영향을 일정하게 유지한 채 연봉과 혈압 간의 관계를 분석해야 '두 변수 간의 진정한 상관관계'를 얻을 수 있음
-> 나이 변수를 통제하면 '연봉과 혈압의 관계'가 사라지게 됨
2) 숨겨진 관계를 찾는 데 활용 (예: 음식섭취량과 몸무게 ~ 운동)
- 두 변수 간의 충분히 예상할 수 있는 기대되는 상관을 발견할 수가 없다면, 다른 변수들이 이 관계를 억제하고 있을 가능성이 존재함
(변수 a 와 변수 b 간에 기대되는 상관이 나타나지 않으면, 변수 a 는 다른 변수 c 와 정의 상관관계를 갖고 이와 동시에 이 변수 c 가 변수 b 와 부의 상관관계를 갖고 있기 때문일 수가 있음.
변수 c 를 통해서 '+ 상관관계' 와 '- 상관관계'가 상쇄가 돼서 변수 a 와 변수 b 간의 관계가 드러나지 않을 수가 있음.)
(예: 와인냉장고에 대한 구매 필요성과 구매 의향 간의 상관관계가 거의 나타나지 않을 때)
: 이때 새로운 변수 '소득'을 고려할 경우에, 소득과 구매 필요성 간에는 '부의 상관관계'가 나타나고, 소득과 구매의향 간에는 '정의 상관관계'가 나타남.
편상관분석을 이용해서 소득의 영향을 통제하면, 즉 '소득을 통제한' 구매필요성과 구매 의향 간의 편상관계수를 구하면, 처음과 달리 '정의 선형관계'를 확인할 수 있음. 결국 '소득'이라는 제 3의 변수로 인해서 '구매 필요성과 구매 의향 간의 관계'가 드러나지 않았다고 볼 수가 있음
- R 을 이용한 편상관계수 구하기 절차 시작!
- 표준 패키지에 포함된 mtcars 데이터셋 이용: 자동차 모델 별로 자동차에 대한 정보가 저장되어 있음
- mpg : 연비, cyl: 실린더의 개수, hp: 마력, wt: 자동차의 무게를 의미함
- cor( ) 함수 이용: 변수의 상관계수 구하는 함수
colnames(mtcars)
# mtcars 데이터셋에서 몇 개 변수만 선택하여 'subset' 생성
mtcars2 <- mtcars[, c("mpg", "cyl", "hp", "wt")]
cor(mtcars2)

[변수들 간의 상관계수 살펴보기]
- 연비 (mpg) 와 자동차 마력 (hp) 간의 상관 계수 : - 0.78 (꽤 높은 수준의 '부의 상관관계' 관찰 가능)
-> 연비와 나머지 두 개의 변수 간의 관계에도 마력 간의 관계 못지 않게 꽤 높은 수준의 '부의 상관관계'가 출력된 것을 볼 수 있음
-> 연비 (mpg) 와 실린더의 개수 (cyl) 간 상관 계수: -0.85
-> 연비 (mpg) 와 자동차 무게 (wt) 간 상관 계수: -0.87
(연비와 자동차 마력 간의 이러한 높은 수준의 '부의 상관관계'가 어쩌면, 연비(mpg)와 실린더 갯수 (cyl) 간의 관계 & 연비(mpg)와 자동차 무게 (wt) 간의 관계에 의한 영향을 받았을 수도 있다는 생각이 듦)
-> 연비 (mpg)와 마력( hp) 간의 순수한 상관관계를 구해서 가능성 확인:
: 실린더 갯수(cyl) 와 무게(wt) 의 영향을 통제한 상태에서 연비(mpg)와 마력(hp) 간의 편상관계수 계산
- 연비와 마력간의 편상관계수 구하기
- ggm 패키지에 포함된 pcor 함수 이용
- 실런더 개수(cyl) 와 자동차 무게(wt) 를 통제한 상태에서 연비(mpg)와 마력(wt) 간의 순수한 상관 계산 식
⭐ BiocManager::install('graph') 기억하기!
install.packages('ggm')
BiocManager::install('graph')library(ggm)
# pcor() 함수의 첫번째 인수: 상관계수를 계산할 변수와 통제할 변수의 인덱스나 변수명 지정
# -> 처음 두 개의 인덱스(변수명): 편상관계수를 계산할 변수를 나타냄, 나머지는 통제할 변수를 의미함
# -> 연비(mpg) 와 마력 (hp) 간의 편상관계수 구하기 : 첫번째와 세번째의 인덱스 지정
# -> 나머지 통제 변수: 실린더 개수(cyl) 와 자동차 무게(wt): 두번째, 4번째 인덱스 지정
# pcor() 함수의 두번째 인수: 공분한 행렬(cov() 함수) 지정
pcor(c(1, 3, 2, 4), cov(mtcars2))
pcor(c("mpg", "hp", "cyl", "wt"), cov(mtcars2))
*인덱스가 아닌 '변수명' 지정도 괜찮음: pcor(c("mpg", "hp", "cyl", "wt"), cov(mtcar2)) *
-> 실린더 개수 (cyl) 와 무게(wt) 를 통제한 연비(mpg) 와 마력(hp) 간의 편상관계수는 '-0.28'로, 연비와 마력 간의 피어슨 상관계수 -0.78 에 비해 거의 3분의 1 수준으로 축소되었음
-> 연비(mpg) 와 마력(wt) 간의 이러한 높은 상관계수는, 실린더 개수(cyl) 와 자동차 무게(wt) 의 영향을 받았을 수 있다 라고 생각해 볼 수 있음
-> 실린더 개수(cyl) 와 자동차 무게(wt) 의 영향을 배제하게 되면, 연비와 마력 간의 순수한 상관관계는 -0.28 로 작아지는 것을 볼 수 있음
- pcor.test( ) 함수: 편상관계수에 대한 유의성 검정하는 함수
# pcor.test()함수의 첫번째 인수: pcor 함수로부터 계산된 편상관계수 지정
# pcor.test()함수의 두번째 인수 (q): 통제할 변수의 개수 지정
# -> 통제 변수: 실린더 개수(cyl) 와 자동체 무게(wt) 를 통제할 변수로 사용했기 때문에 q 인수 의미를 지정
# pcor.test()함수의 세번째 인수 (n): 관측값의 개수(표본크기) 지정
pcor.test(pcor(c(1, 3, 2, 4), cov(mtcars2)), q=2, n=nrow(mtcars2))
-> 검증결과: 0.14/ p 값을 유의수준 0.05 에 비교했을 때, 유의수준 보다 크기 때문에 '귀무가설 채택'
(순수한 상관관계는 모집단에서 0일 가능성 있음)
-> 귀무가설: 모집단에서 편상관계수가 '0' 이다
-> 실린더 개수(cyl) 과 자동차 무게(wt)를 통제하면 -> 연비(mpg) 와 마력(hp) 간의 순수한 상관관계는 존재하지 않음
-> 두 변수 간의 드러난 상관관계는 상당부분, 실린더 개수와 무게로 인한 것이라고 판단 가능

-> 이름이 같아서!
- detach(pacakge: ggm) or ppcor::pcor(mtcar2)
- ppcor 패키지: 편상관계수에 대한 유의성 검증 수행하는 패키지
- pcor 함수: 모든 변수 간의 편상관계수와 그에 대한 유의 확률을 구할 수 있는 함수
library(ppcor)
detach(package:ggm)
# pcor()함수의 인수: 행렬이나 데이터프레임을 인수로 지정
# -> 모든 변수 간의 편상관계수와 그에 대한 유의확률 p-값 계산
# -> 이때, 편상관계수 산출에 포함된 변수 이외의 나머지 다른 변수는 통제변수로 간주됨
pcor(mtcars2)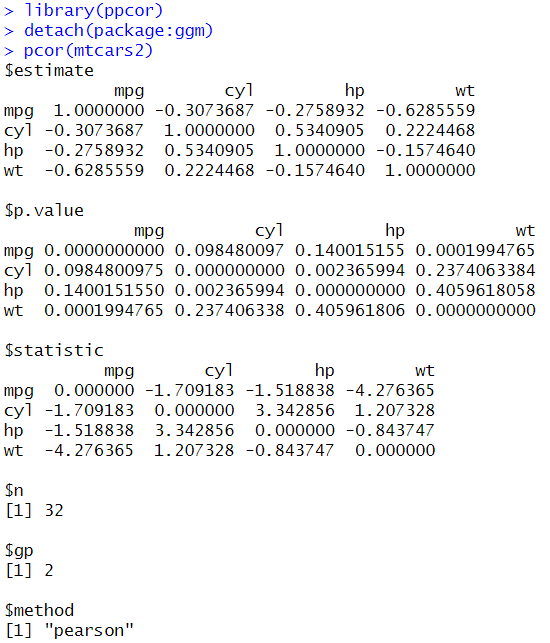
[출력결과]
1) 모든 변수 쌍 간의 편상관계수를 볼 수 있음
2) 편상관계수에 대한 유의확률도 확인
-> 각 변수 쌍 간의 편상관게수를 산출할 때, 나머지 변수들은 통제 변수로서 간주됨
-> 연비(mpg) 변수와 마력(hp) 변수 간의 편상관게수를 계산: 나머지 2개 변수 (실린더 개수_ cyl 변수와 자동차 무게_wt 변수가 통제변수로써 사용됨)
-> 연비(mpg) 변수와 실린더 개수(cyl) 변수 간의 편상관게수를 계산: 나머지 2개 변수 (마력_hp 변수와 자동차 무게_wt 변수가 통제변수로써 사용됨)
- pcor.test( ) 함수: 모든 변수 쌍이 아니라 특정 두 변수 만의 편상관계수 유의 확률을 계산하는 함수
# pcor.test() 함수의 첫번째, 두번째 인수: 편상관계수를 계산하려는 변수를 차례대로 지정
# -> 이 두개의 변수: 편상관관계를 계산하는 대상 변수가 됨
# pcor.test() 함수의 세번째 인수: 통제변수 지정(위 두개의 변수 제외한)
pcor.test(mtcars2["mpg"], mtcars2["hp"], mtcars2[c("cyl", "wt")])
-
자료출처: https://github.com/kykwahk/Statistics-R/blob/master/Statistics-R_06.R
Statistics-R/Statistics-R_06.R at master · kykwahk/Statistics-R
『R을 이용한 통계데이터분석(제2판)』(곽기영, 도서출판 청람). Contribute to kykwahk/Statistics-R development by creating an account on GitHub.
github.com
https://www.youtube.com/watch?v=LKK9PaSu9zU
'통계' 카테고리의 다른 글
| [통계 데이터 분석] 독립성검정과 적합성검정 (0) | 2024.11.02 |
|---|---|
| [통계 데이터 분석] 상관분석-자체 (0) | 2024.10.28 |
| [통계 데이터분석] 공분산분석, 반복측정 분산분석, 다변량 분산분석 (0) | 2024.10.17 |
| [통계 데이터분석] 분산분석- 이원분산분석 (0) | 2024.10.17 |
| [통계 데이터분석] 분산분석- 일원분산분석 (0) | 2024.10.16 |



